射频 - 谐振电路 - 无损组件的共振

在之前的章节，我们在基本元器件的寄生器件中提到了共振。以下将研究共振产生的原因及如何利用它。

无损组件的共振

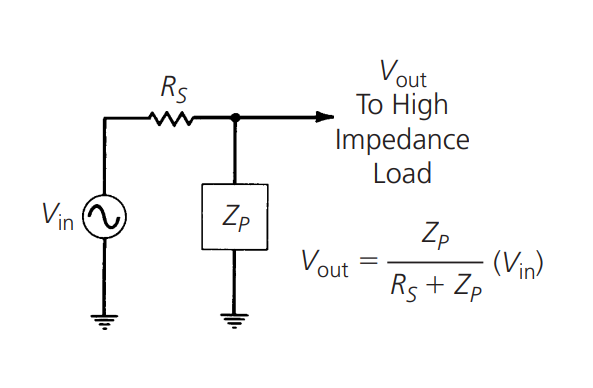
从上图的分压规则可以看出，当阻抗为 \(Z_p\) 的分流元件放置在具有内阻 \(R_s\) 的发生器的输出端时，该电路可达到的最大输出电压为：

\[ V_{out}=\frac{Z_p}{R_s+Z_p}(V_{in}) \]

因此，\(V_{out}\) 始终小于 \(V_{in}\)。如果 \(Z_p\) 是与频率相关的阻抗（例如容性或感性电抗），则 \(V_{out}\) 也将与频率相关，并且 \(V_{out}\) 与 \(V_{in}\) 的比率是电路的增益（或在这种情况下为损耗），也将取决于频率。例如，我们以一个 25pF 电容器作为分流元件:

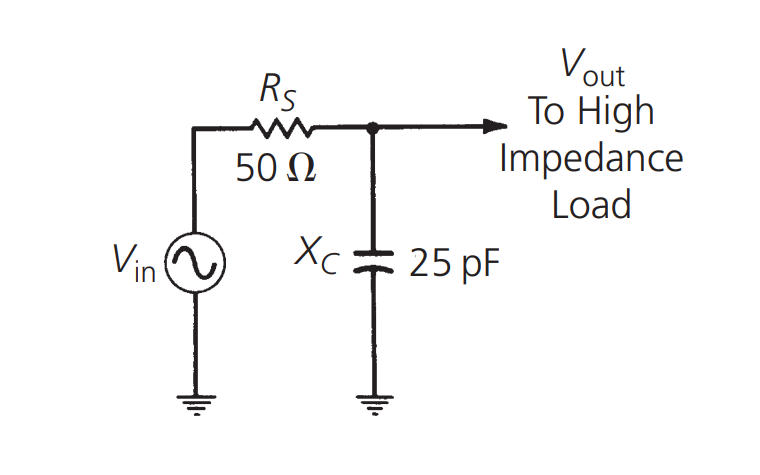
并绘制 \(V_{out}/V_{in}\) 函数（以 dB 为单位）与频率的关系：

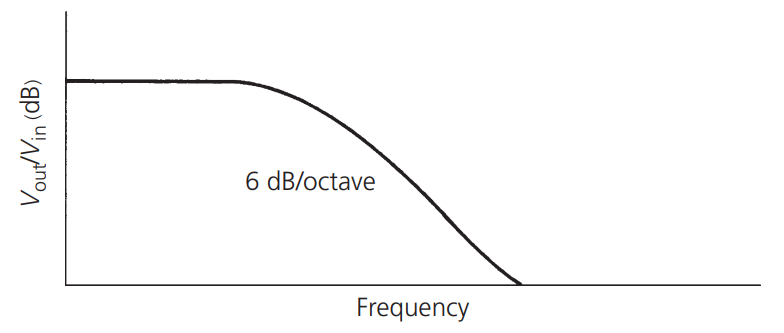
依据以下的公式：

\[ \frac{V_{out}}{V_{in}}=20\log_{10} \frac{X_C}{R_s+X_C} \]

其中，\(\frac{V_{out}}{V_{in}}\) 是以 dB 表示的损耗；\(R_s\) 表示源阻抗；\(X_C\) 表示容抗，\(X_C=\frac{1}{j\omega C}\)。

此 RC 电路的损耗会随着频率的增加而增加。这就形成了一个简单的低通滤波器。需要注意的是，频率每翻一倍，衰减斜率会以 6 dB 的速率下降。这是由于电路中的单个电抗元件导致的。下文将会看到，对于我们加进电路中的每个重要电抗元件，该衰减斜率将额外增加 6 dB。

如果我们把电路中的电容换成一个 0.05µH 的电感：

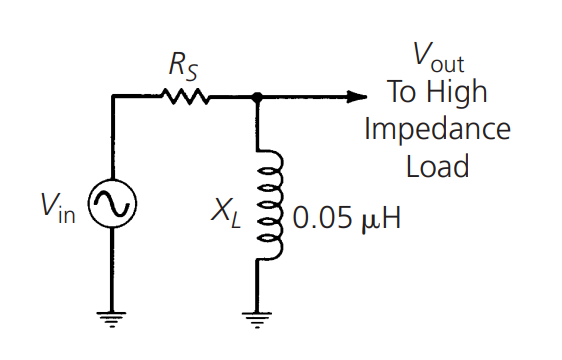
可以绘制出这样的曲线：

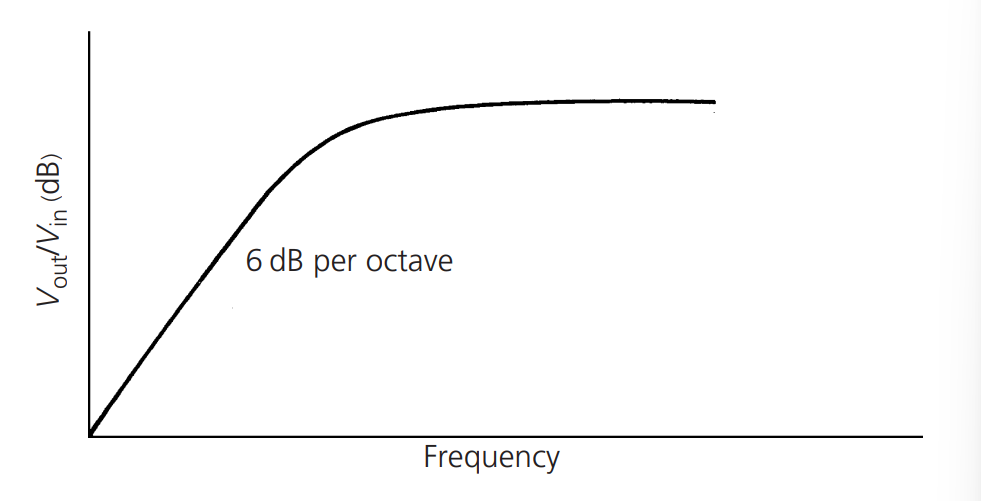
依据的是以下公式：

\[ \frac{V_{out}}{V_{in}}=20\log_{10} \frac{X_L}{R_s+X_L} \]

其中，\(X_L\) 表示感抗，\(X_L=j\omega L\)。

这里形成了一个最终衰减斜率为 6 dB/倍频程的简单高通滤波器。

根据上文的公式，我们能够绘制出两个独立且相反的电抗元件的频率响应。如果我们将电感和电容同时并进源端，形成一个 LC 电路：

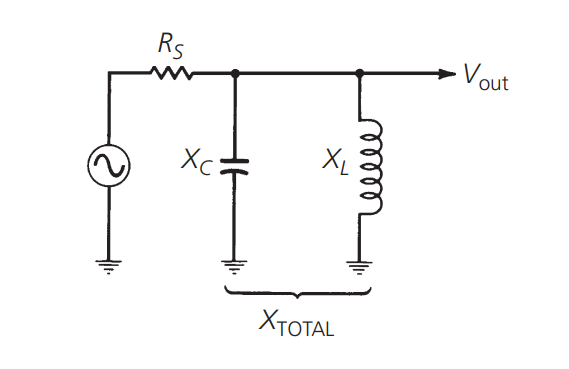
我们将得到这样的曲线：

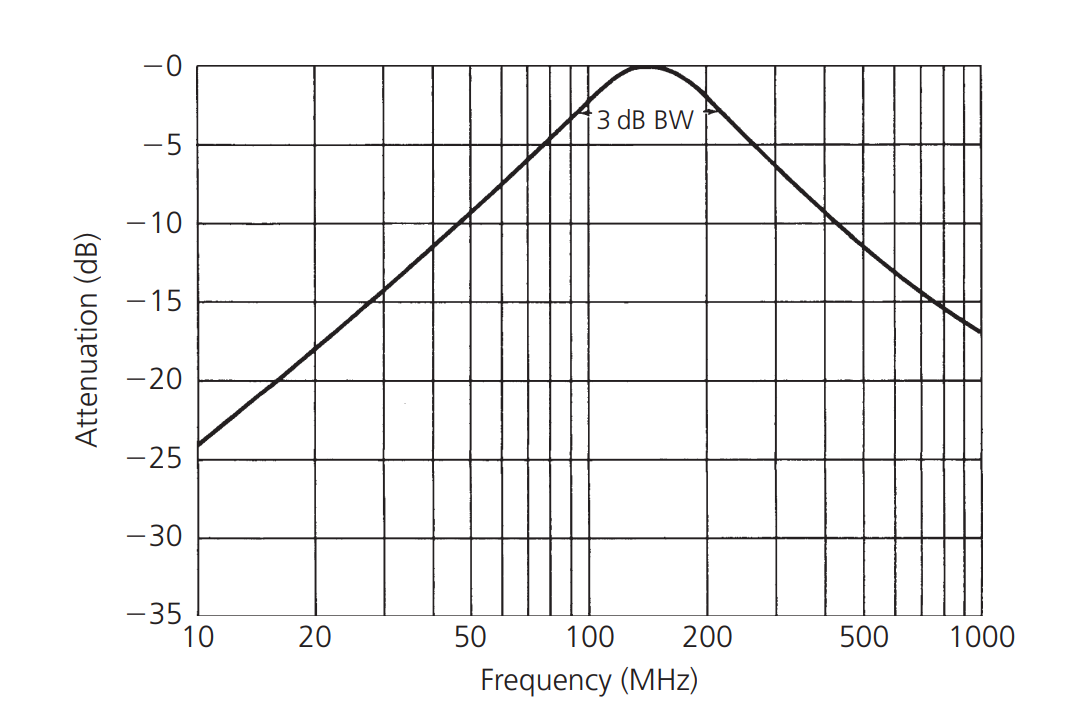
根据以下公式计算而得的：

\[ \because V_{out}=\frac{X_{total}}{R_s+X_{total}}(V_{in}) \]

\[ \because X_{total}=\frac{X_C*X_L}{X_C+X_L} \]

\[ \because X_C=\frac{1}{j\omega C} \]

\[ \because X_L=j\omega L \]

\[ \therefore \frac{V_{out}}{V_{in}}=\frac{j\omega L}{(R_s-\omega^2 R_s L C)+j\omega L} \]

如果用 dB 表示，可以表示为：

\[ \frac{V_{out}}{V_{in}}= 20\log_{10} | \frac{j\omega L}{(R_s-\omega^2 R_s L C)+j\omega L} | \]

在上面的曲线中，当我们接近调谐电路的谐振频率时，谐振曲线的斜率增加到 12 dB/倍频程，这是因为两个电抗元件都在以 6 dB/倍频程的速率变化，并以相反的方向倾斜；然而，当我们在任一方向远离共振时，曲线再次稳定到 6 dB/倍频程的斜率，因为只有一个电抗发挥作用，另一个电抗在这些频率下对电路呈现非常高的阻抗，且在电路中表现几乎可以忽略。

RLC 滤波器可用于从环境无线电波的总频谱中选择某个窄范围的频率，作为带通滤波器使用。

参考与致谢

《RF-Circuit-Design(second-edition)_Chris-Bowick》

原文地址：https://wiki-power.com/
本篇文章受 CC BY-NC-SA 4.0 协议保护，转载请注明出处。