النزاهة في الإشارات - خطوط النقل 🚧
خطوط النقل هي عبارة عن عناصر مثالية، تتألف من أي زوجين من الأسلاك ذات الأطوال المحددة، يطلق عليهما عادة اسم مسار الإشارة والمسار العائد (المسار المرجعي) على التوالي. تحمل خطوط النقل سمتي خاصتين: المقاومة الطابعية والتأخير.
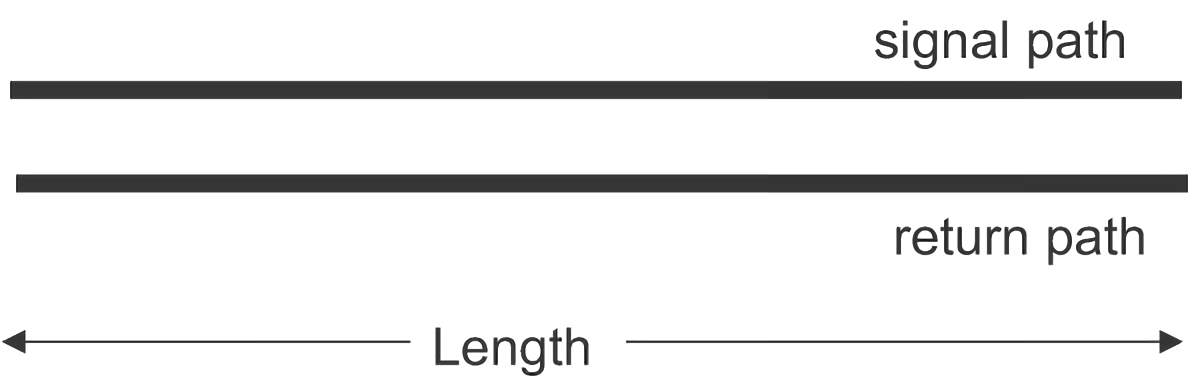
طرق نقل الإشارة
لفهم كيفية نقل الإشارات، يجب مراقبة مسار الإشارة والمسار العائد بشكل متزامن. كيف يمكن تحديد مسار الإشارة والمسار العائد؟ إذا كانت الأسلاكان متماثلتين تمامًا (مثل أسلاك الزوج الملتوي)، فلا يوجد تمييز دقيق؛ وإذا كانت أسلاك النقل من النوع الميكروي، عادة ما يتم تحديد السطح كمسار عائد. يجب ملاحظة أنه في سياق النزاهة في الإشارات، نستخدم مفهوم "المسار العائد" بدلاً من "الأرض"، لأن السيناريوهات التحليلية أكثر تعقيدًا بكثير من مجرد "الأرض".
عندما تدخل الإشارة في خط النقل، تنتقل داخله بسرعة الضوء في وسط الانتقال. يمكن تمثيل الإشارة على مسار الإشارة والمسار العائد على أنها فرق الجهد بين نقطتين متجاورتين:
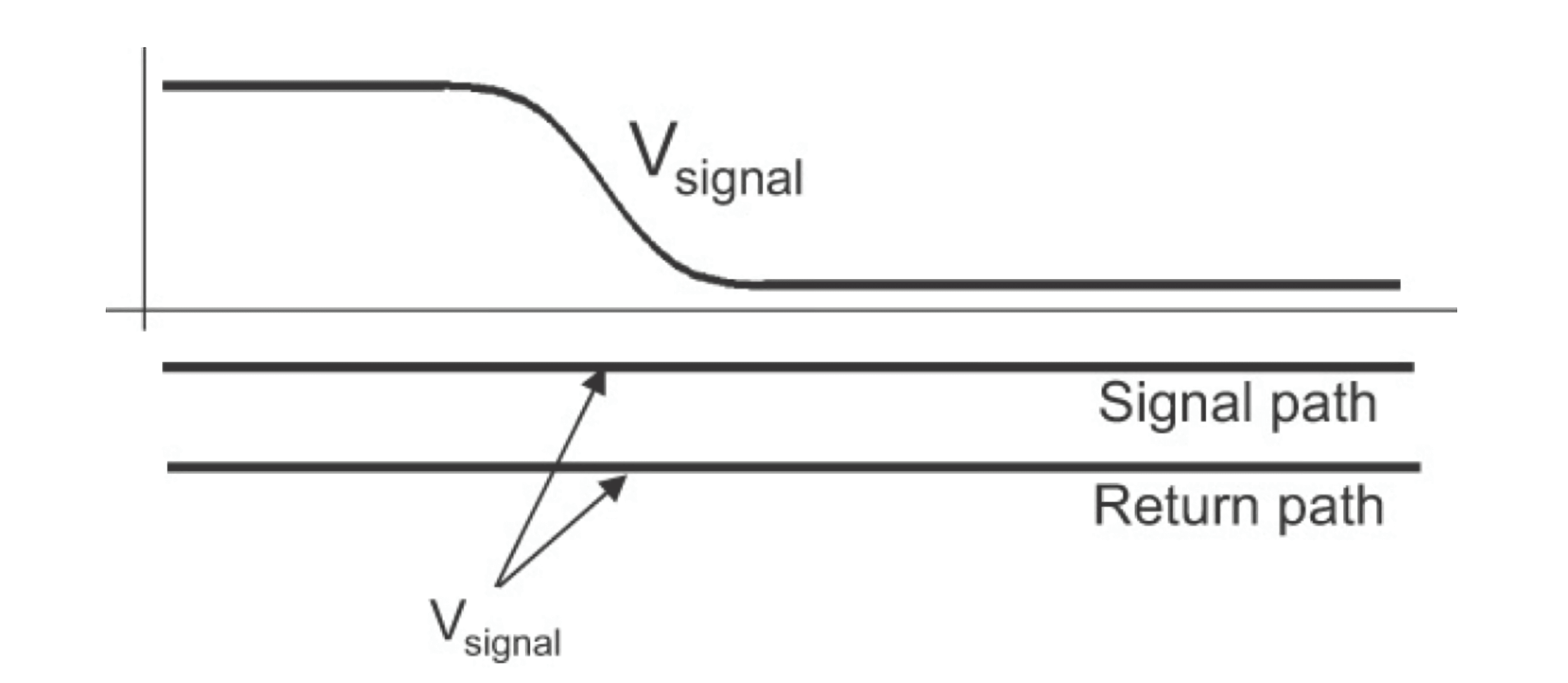
إذا افترضنا زوجًا من الخطوط النقل بمسار طويل ومتصلة بأطراف مفتوحة، ثم قمنا بتوصيل عداد تيار في الطرفين الأصلي والنهائي، يمكننا مشاهدة أنه في التجربة العملية، عندما تدخل الإشارة مسار الإشارة لأول مرة، يتم رصد تيار في المسار العائد بالفعل. لذا، الدائرة الكهربائية للتيار ليست من البداية إلى النهاية من الطرف الأصلي إلى النهاية، ثم عائدة من خلال المسار العائد. بل هي ناتجة عن الفرق في الجهد الكهربائي الذي يتم إنتاجه بين المسار والمسار العائد (مشابهة لشحن الكاباسيتور). مع تقدم الإشارة، تتغير مواقع توليد التيار أيضًا تدريجيًا.
الخطوط النقل المتجانسة والمتوازنة
يمكن تصنيف الخطوط النقل بناءً على هياكلها الهندسية إلى خطوط نقل متجانسة وخطوط نقل متوازنة. هذا التصنيف يستند إلى مدى تشابه مقاطع الخط ومدى تشابه وتناظر الأسلاك.
إذا كانت مقاطع الأسلاك متماثلة في أي موقع على طول الخط، يُعرف بأنها "خط نقل متجانس" أو "خط نقل قابل للتحكم"، مثل أسلاك الزوج الملتوي وخطوط الشريط الميكروي:
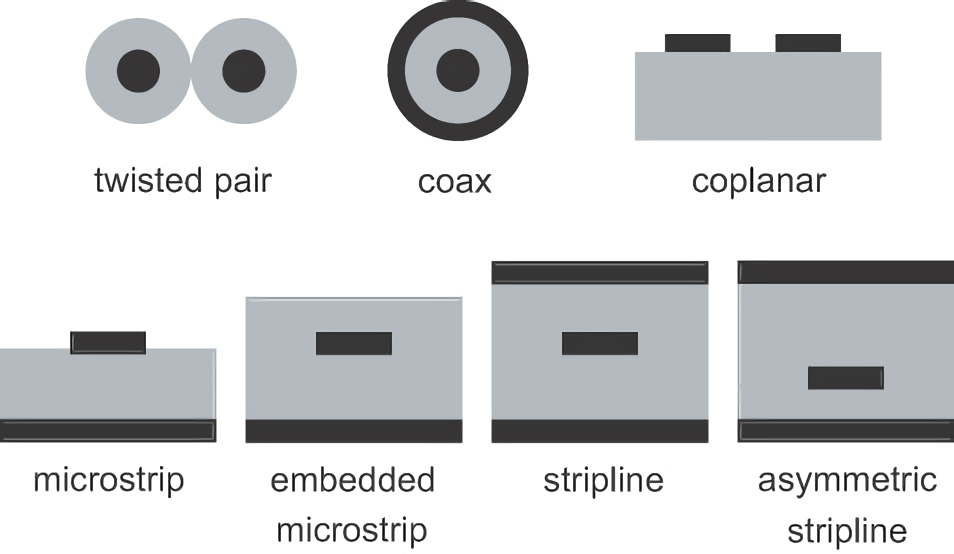
أحد أهداف تصميم النزاهة في الإشارات هو جعل جميع اتصالات السرعة العالية تكون خطوط نقل متجانسة والعمل على تقليل طول جميع الخطوط غير المتجانسة بقدر الإمكان.
السمة الأخرى للتصنيف تتمثل في درجة تشابه أسلاك النقل. إذا كانت أسلاك النقل متشابهة في الشكل والحجم، فإنها تُعرف بأنها "خطوط نقل متوازنة"، مثل أ
يمكن تصور السلك كأنه أنبوب طويل مليء بالكرات، إذا تم دفع كرة واحدة في أحد الأطراف، فإنه سيتم دفع كرة أخرى تقريبًا في الطرف الآخر في نفس الوقت. في هذا المكان، سرعة انتقال الإشارة بواسطة الكرات أسرع بكثير من سرعة حركة الكرات بالفعل. بالمثل، عندما يتأثر الإلكترون داخل السلك بتأثير من الإلكترونات المجاورة، فإن سرعة انتقال الإشارة لا تعتمد على سرعة حركة الإلكترون بذاته، بل تتأثر بالتداخل بين هذه الإلكترونات.
عند نقل الإشارة، تنشأ حول السلك وفي الفضاء المحيط بالسلك مجالات كهرومغناطيسية متناوبة. والعامل الذي يحدد سرعة انتقال الإشارة هو سرعة إنشاء وانتقال هذه المجالات الكهرومغناطيسية.
يمكن حساب سرعة التغيير في مجال المجال الكهرومغناطيسي (سرعة سلسلة المجال) باستخدام الصيغة التالية:
حيث تمثل \(\varepsilon_0\) الثابت الكهربائي في الفضاء الحر، والذي يكون قيمته \(8.89 \times 10^{-12} F/m\)؛ وتمثل \(\varepsilon_r\) الثابت الكهربائي النسبي للمواد، والذي يكون 1 في الهواء؛ وتمثل \(\mu_0\) معامل الاستقطاب المغناطيسي للفضاء الحر، والذي يكون قيمته \(4\pi\times10^{-7}H/m\)؛ وتمثل \(\mu_r\) الثابت المغناطيسي النسبي للمواد، ويكون تقريباً 1 في معظم وسائل الاتصال بين الأجهزة. بعد تعويض هذه القيم الثابتة، يمكن الحصول على العلاقة التالية:
بالمقارنة مع الهواء، قيم الثابت الكهربائي \(\varepsilon_r\) للمواد الأخرى عادة تكون أكبر من 1، وسرعة الضوء تقريباً تساوي 12 بوصة في النانوثانية، وبالتالي يمكن القول إن سرعة الإشارة في وسائل الاتصال تكون دائماً أقل من 12 بوصة في النانوثانية، ويمكن حساب السرعة الفعلية كما يلي:
يُشار إلى الثابت الكهربائي النسبي أحيانًا بالثابت الكهربائي، وقيمه غالباً ما تكون 4 لمعظم البوليمرات. عادةً ما ينخفض الثابت الكهربائي مع زيادة التردد، لكن الفروق في الثابت الكهربائي في مواد لوحات الدوائر المطبوعة الشائعة ليست كبيرة. على سبيل المثال، يتراوح ثابت الكهربائي لل FR4 بين 3.5 و 4.5، بينما يتراوح لوحات الدوائر السريعة في المعدل بين 3 و 4. بناءً على الصيغة، يمكن أن نستنتج أن سرعة الإشارة في FR4 تكون حوالي 6 بوصة في النانوثانية (دون مراعاة تأثير مجال كهرومغناطيسي الهواء).
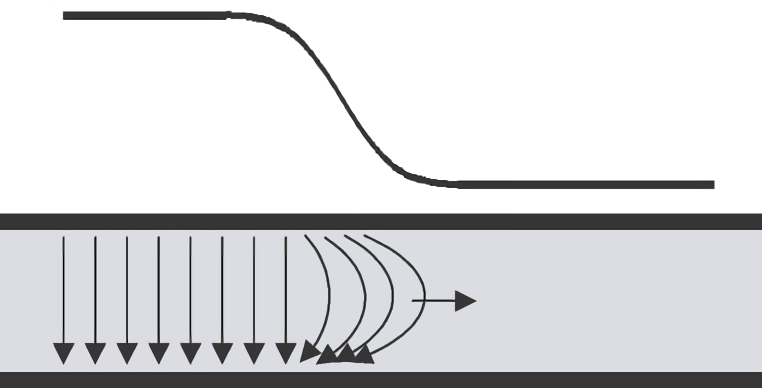
تمديد الفضاء المقدم
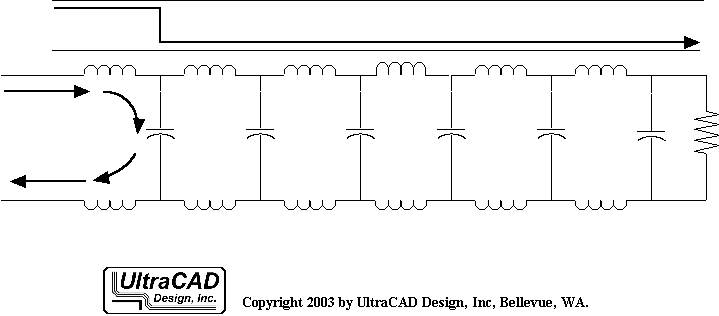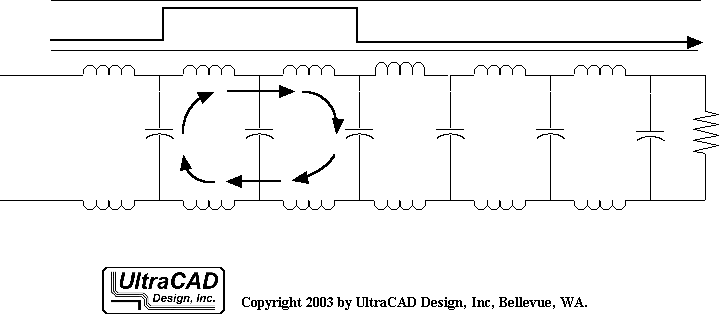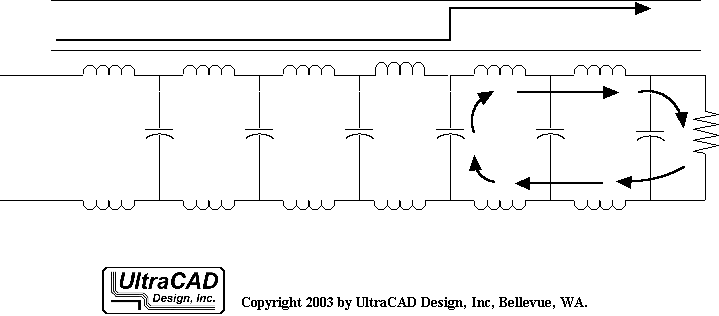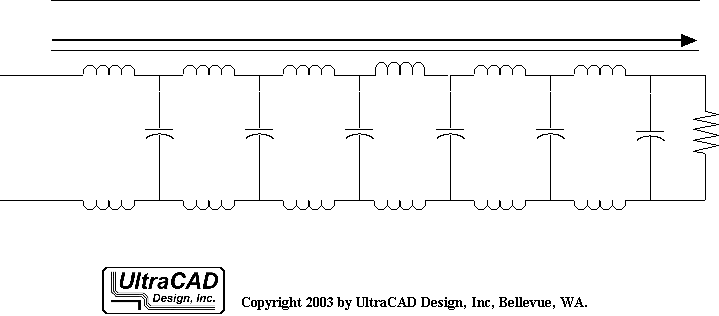
يُمثل ارتفاع الإشارة RT عادة الوقت اللازم للإشارة للتغير من 10٪ إلى 90٪ من الجهد الكهربائي القصوى. عندما تنتقل الإشارة عبر الخطوط الناقلة، يتم دفع هذا
بسبب أن خط النقل يمكن أن ينظر إليه ككيان واحد يجمع بين إشارة والمسار العائد ككيان واحد، حيث يوجد تيار الإشارة وتيار العائد في وقت واحد ويشكلان دائرة تيار كاملة، فإن تحليل التماثل الدائري سيكون أكثر سهولة. وصيغة حساب المؤثر الدائري هي:
حيث، \(L_{SS}\) يمثل التفاضل الذاتي للمسار الإشاري، \(L_{FS}\) يمثل التفاضل الذاتي للمسار العائد، و \(L_{SFm}\) هو التفاضل المتبادل بين المسار الإشاري والعائد.
باعتبار الدائرة ككيان واحد، فإن مصفوفة الدائرة تصف خصائص التفاضل الدائري للدائرة نفسها، وهذا يعادل التفاضل الذاتي للدائرة نفسها.
التفاضل الوحدة
من أجل تبسيط النمذجة، يمكن أيضًا تكافؤ التفاضل الكهربائي لخط النقل على أنه يتكون من عدة تفاضل متصلة تتسلسل. عند تقسيم خط النقل إلى وحدات تفاضل صغيرة (تحتوي كل وحدة على مسار إشارة وعائد) بطول \(\Delta Z\)، فإن زيادة \(\Delta Z\) ستؤدي إلى زيادة مساحة المنطقة التي تتكون منها إشارة المنطقة ومسار العودة، وبالتالي زيادة كمية التدفق المغناطيسي. نظرًا لأن التدفق المغناطيسي يتناسب بشكل خطي مع مساحة المنطقة \(\Delta Z\)، فإنه يتناسب بشكل خطي أيضًا مع \(\Delta Z\). ولذلك، بمجرد معرفة التفاضل الدائري للوحدة، يمكن الحصول على التفاضل الدائري لأي طول من التفاضل.
مقاومة التأثير الزمني والمقاومة الخاصة √
بناءً على التعريف السابق، نعلم أن المقاومة تشير إلى نسبة الجهد إلى التيار في موقع معين على خط النقل. نظرًا لأن خط النقل ليس دائمًا موحدًا، يمكن أن تكون المقاومة التي يواجهها الإشارة عند كل خطوة مختلفة. هذه هي نوع من المقاومة الزمنية.
إذا كان خط النقل موحدًا، فيمكن تمثيل خصائص المقاومة بقيمة واحدة تسمى "المقاومة الخاصة" لخط النقل. يمكن تمثيل المقاومة الخاصة بواسطة وحدات التفاضل ووحدات التيار:
المقاومة الخاصة هي ما نشهد استخدامها عادة عند تصميم PCB بقيمة 50 أوم، والتي تعني المقاومة الخاصة. بالنسبة للوحة FR4، عندما تكون عرض الخط مضاعفة سمك العازل، فإن مقاومة خط النقل المجوف تكون 50 أوم. عندما يكون تباعد خطوط النقل متساويًا، كلما زادت المقاومة الخاصة، زادت مشكلة التداخل. بينما كلما قلت المقاومة الخاصة، زادت فقدانات الطاقة. لذلك، الاعتماد على 50 أوم هو خيار متوازن نسبيًا، ولا يعني ذلك أن كل الاتصالات بالضرورة 50 أوم، يمكن تخصيص مقاومة خط النقل وفقًا للحاجة.
عوامل تأثير المقاومة الخاصة √
هناك أربعة عوامل رئيسية تؤثر في المقاومة الخاصة: "عرض الخط، سمك العا
إذا كان المسار العائد هو مستوٍّ (على نفس المستوى)، وليس على نفس الطبقة كمسار الإشارة، يُطلق عليه اسم المستوى المرجعي. بالنسبة للمسارات السطحية للإشارات، يمكن أن تتكون الخطوط النقل فقط مع المستوى المرجعي المجاور، ويمكن القول أن المسارات السطحية للإشارات لديها مستوى مرجعي واحد فقط. وبالنسبة للمسارات الداخلية، هناك مستويين مرجعيين مجاورين من الأعلى والأسفل، لذلك هناك مستويين مرجعيين. يمكن استخدام أي مستوى يقع في طبقة مختلفة ويتداخل مع مسار الإشارة كمستوى مرجعي، وبذلك يتم تكوين خط نقل.
ليس توزيع التيار العائد على المستوى المرجعي موزونًا على مدى المستوى بأكمله، بل لديه تأثير تردد الجلد وسيكون مكتظًا بالقرب من موضع المسار. التيار العائد على المستوى المرجعي لخط النقل السطحي يكون بنفس حجم التيار الإشارة. أما بالنسبة للخطوط النقل ذات الشريط، فإنه نظرًا لوجود مستويين مرجعيين من الأعلى والأسفل، سيكون التيار العائد متمركزًا حول منطقة الجزء العلوي والسفلي لخط الإشارة، وسيتم توزيعه نسبيًا وفقًا للمسافة إلى المستوى. كلما زادت ترددات الإشارة، زاد تكتل التيار.
تأخير الخطوط النقل 🚧
تحتاج الإشارة إلى وقت معين للوصول من نقطة المصدر إلى نقطة الوجهة، وهناك تأخير محدد.
النموذج الأولي للخطوط المثالية 🚧
الخطوط النقل المثالية لديها خاصتين مهمتين: المعاوقة اللحظية الثابتة والتأخير المقابل. يستند النموذج الأولي إلى النموذج الصفري بأنه يُجرى تجريد لكل قسم صغير من الإشارة والمسار العائد كملف انتقالي:
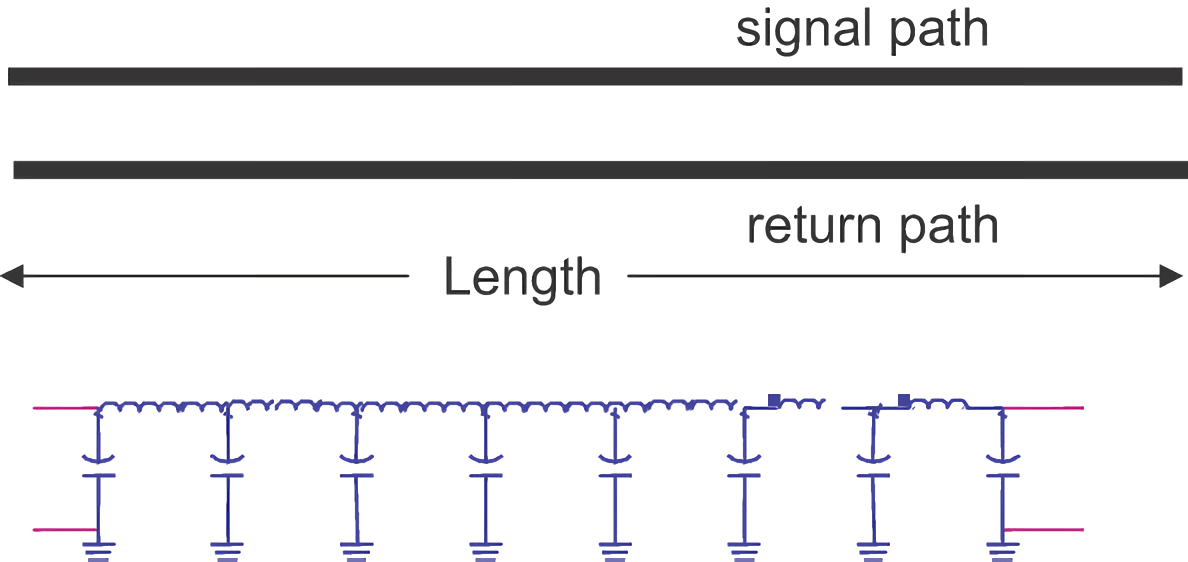
عندما يكون السعة واللفائف صغيرة للغاية، وعندما يصبح عدد مقاطع LC غير محدود، تتجه السعة اللحظية للوحدة \(C_L\) واللفائف اللحظية للوحدة \(L_L\) نحو ثوابت لخصائص الخطوط النقل. إذا كانت الطول الإجمالي للخطوط النقل هو \(Len\)، فإن السعة الإجمالية واللفائف الإجمالية تكون:
لذا، معاوقة الخطوط النقل والتأخير \(Z_0\) و\(T_D\) على النحو التالي:
بما أن معاوقة الخطوط النقل والتأخير يجب أن يكونا متسقين مع نتائج النموذج الصفري، يمكن الحصول على بعض المعادلات المرتبطة.
نظرًا لأن سرعة الإشارة تعتمد على الثابت الكهروضوئي للمادة \(\varepsilon_r\) (إبسيلون الصوت) وتعتمد على السعة واللفائف للوحدة، يمكن الحصول على المعادلة التالية:
المراجع والشكر
- "تحليل سلامة الإشارات وتحليل سلامة الطا
تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.