النزاهة في الإشارة - في المجال الزمني والترددي

بشكل عام، نقوم بتحليل الإشارة من منظورين مختلفين: المجال الزمني والمجال الترددي.

المجال الزمني

المجال الزمني هو المجال الذي يظهر فيه العالم الحقيقي بتسلسل زمني. على سبيل المثال، في رسم الإشارة في المجال الزمني لإشارة ساعة معينة، يمكن مشاهدة معلمتين مهمتين، وهما فترة الموجة وارتفاع الحافة:

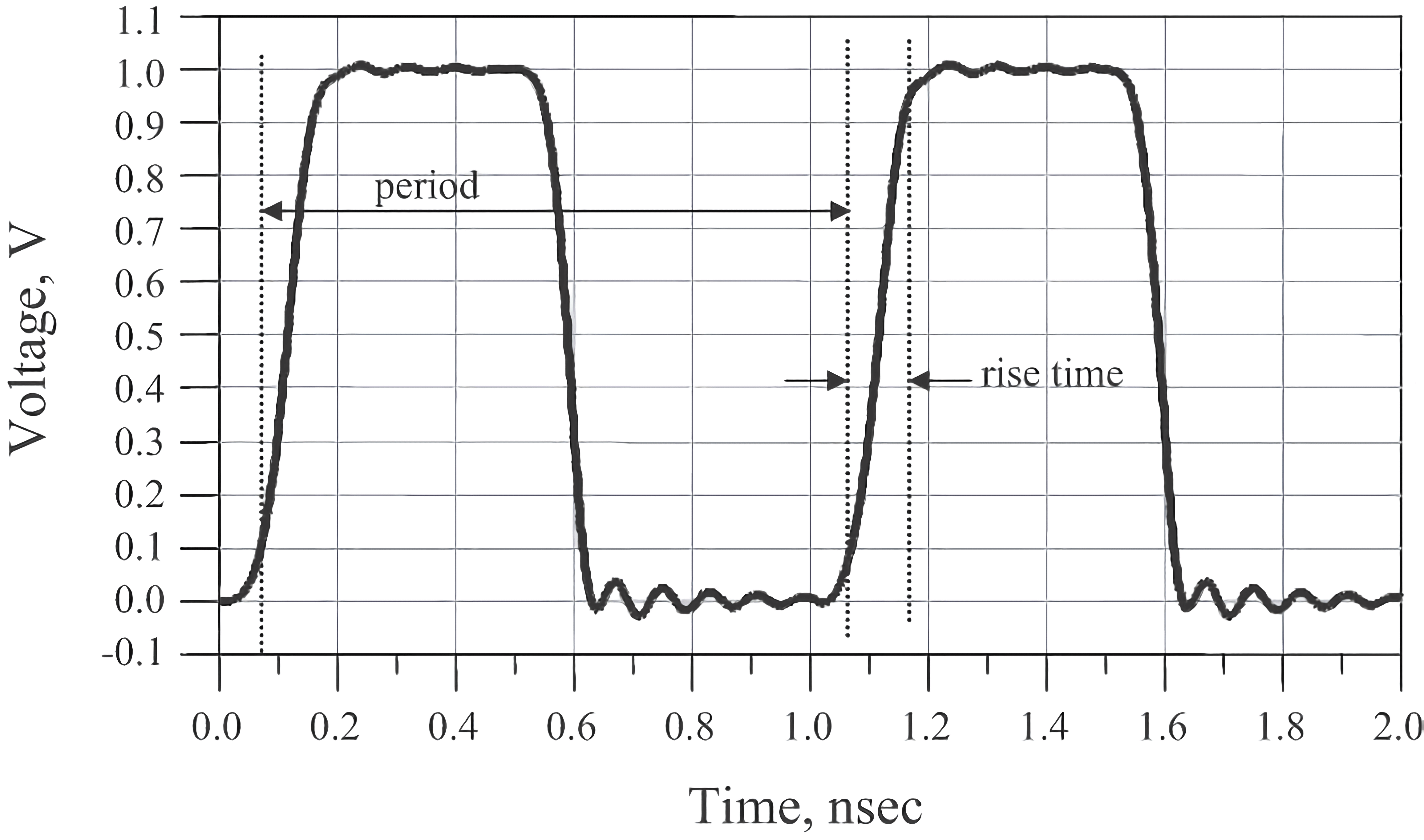
فترة الساعة هي الزمن الذي يستغرقه تكرار الإشارة مرة واحدة، وعادة ما تكون وحدتها نانوثانية. تردد الساعة هو عدد مرات التكرار في الثانية الواحدة، وهو عكس الفترة. على سبيل المثال، لإشارة ساعة بفترة 1 نانوثانية، يكون التردد هو 1/10 نانوثانية = 0.1 غيغاهرتز.

الارتفاع يُعرف عادة على أنه الزمن الذي يستغرقه الإشارة للانتقال من 20٪ إلى 80٪ من أعلى القمة (أحيانًا يمكن تعريفه كـ 10٪ إلى 90٪). الهبوط عادة ما يكون أقل من الارتفاع، وذلك لأنه في الهياكل النمطية النموذجية CMOS، الجهد العالي لل-NMOS ينخفض بسرعة أكبر من الجهد العالي لل-PMOS، وبالتالي الهبوط يكون عادة أقصر من الارتفاع، وهذا يجعله أكثر عرضة لمشاكل النزاهة في الإشارة.

المجال الترددي

المجال الترددي هو مجال موجود في الرياضيات. عادة ما يتم استخدام الموجات الجيبية في المجال الترددي، لأن أي شكل موجي في المجال الزمني يمكن تحليله إلى موجات جيبية.

يمكن وصف المعلومات بشكل أكثر إيجازًا في المجال الترددي. كما هو موضح في الصورة أدناه، يمكن وصف الموجة الجيبية في المجال الزمني على الجانب الأيسر، ويمكن تمثيل التردد والتعزيز بنقطة واحدة فقط في المجال الترددي (عادة يتم تجاهل المرحلة في معظم الحالات):

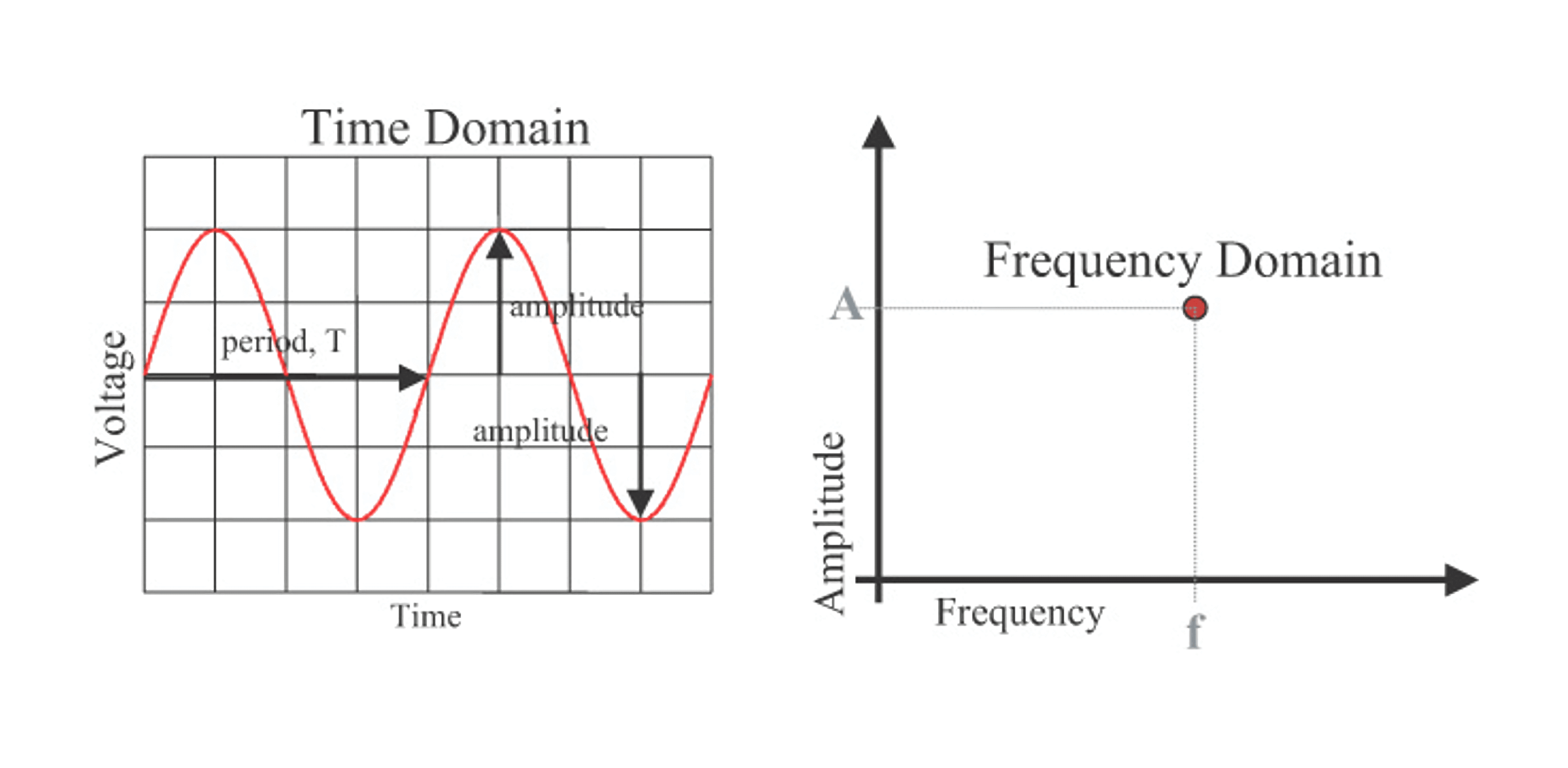
بهذه الطريقة، يمكن تمثيل الموجة الجيبية في المجال الترددي بمجرد نقطة واحدة. إذا كان هناك عدة نقاط تمثل ترددات مختلفة، يُشار إليهذا التجمع بأنه الطيف الترددي.

توضح العملية أن نقل المشاكل الكهربائية العامة إلى المجال الترددي واستخدام الموجات الجيبية يجعل من السهل فهمها وحلها.

التحول من المجال الزمني إلى المجال الترددي

للانتقال من المجال الزمني إلى المجال الترددي، يتم استخدام تحول فورييه. هناك ثلاثة أنواع من تحولات فورييه: تحول فورييه (FI)، تحول فورييه مكتوم (DFT)، وتحول فورييه السريع (FFT).

تحول فورييه يُستخدم لتحويل التعبيرات الرياضية المثالية في المجال الزمني إلى تمثيل في المجال الترددي. يشمل هذا تكامل المجال الزمني عبر محور الزمن من ناقص اللانهائي إلى إيجابي اللانهائي للحصول على دالة متواصلة في المجال الترددي من الصفر إلى إيجابي اللانهائي.

ومع ذلك، يتمثل الشكل الزمني الفعلي في تكوين مجموعة من النقاط المتناثرة. في هذا السياق، يمكن استخدام تحول فورييه مكت

وفقًا للقاعدة التجريبية المشتقة، فإن العلاقة بين النطاق الترددي وارتفاع الارتفاع هي BW = 0.35 / RT، حيث BW هو النطاق الترددي (جيجاهرتز) و RT هو ارتفاع الارتفاع من 10% إلى 90% (نانوثانية). كمثال، إذا كان ارتفاع الارتفاع للإشارة هو 0.1 نانوثانية، فإن النطاق الترددي للإشارة سيكون 0.35 جيجاهرتز، والعكس صحيح. (يرجى ملاحظة توافق الوحدات، حيث تتوافق جيجاهرتز مع نانوثانية وميجاهرتز مع ميكروثانية).

المراجع والشكر

• "تحليل سلامة الإشارة وسلامة الطاقة"
• شرح سلسلة أساسيات تحويل فورييه وتحليله
• سلسلة أساسيات تحويل فورييه

عنوان النص: https://wiki-power.com/
يتم حماية هذا المقال بموجب اتفاقية CC BY-NC-SA 4.0، يُرجى ذكر المصدر عند إعادة النشر.

تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.