النزاهة في الإشارات - المعاوقة والنموذج الكهربائي

المعاوقة (المعاوقة الكهربائية، Z) هي مصطلح يُستخدم للإشارة إلى التأثير الكلي للمقاومة والملف والمكثف في الدوائر الكهربائية على تدفق التيار المتردد، وهي تُعرف بأنها نسبة الجهد إلى التيار (Z = V/I). المعاوقة هي عبارة عن عدد مركب، والجزء الحقيقي يُعرف بالمقاومة، والجزء الخيالي يُعرف بالمعاوقة. يُطلق على التأثير الذي يُمارسه المكثف في الدائرة الكهربائية على تدفق التيار المتردد مصطلح معاوقة السعة، بينما يُعرف تأثير الملف على تدفق التيار المتردد بمعاوقة اللفظ. ويُشكل مجموع معاوقة السعة ومعاوقة اللفظ المعاوقة الكهربائية.

بالنسبة للجهد الثابت، كلما زادت المعاوقة، قل التيار الناتج عنها، والعكس صحيح. في الحالات القصوى، تكون معاوقة الدائرة المفتوحة لا متناهية، بينما تكون معاوقة الدائرة المقفلة صفر. في حالة الأسلاك المتصلة، تعتبر المعاوقة عاملًا رئيسيًا يؤثر على الإشارات. أثناء انتشار الإشارات، يتعين على النظام التفاعل باستمرار بناءً على المعاوقة الفورية.

النموذج الكهربائي الأساسي

أثناء بناء النموذج الكهربائي الأساسي، نفكر في هذه الأنواع الخيالية من العناصر ذات المنفذين:

المقاومة الكهربائية الخيالية.
المكثف الكهربائي الخيالي.
الملف الكهربائي الخيالي.
الخط المثالي للنقل.

من بين هذه العناصر، يمكن تجميع خصائص المقاومة والسعة واللفظ إلى نقطة واحدة، لذا يُطلق عليها "عناصر الدائرة المجمعة". الهدف هو بناء نموذج دائرة مكافئ يجعل المعاوقة تكون مماثلة قدر الإمكان للمعاوقة المقاسة للعناصر الفعلية.

المعاوقة الزمنية للمقاومة الكهربائية

المعاوقة الكهربائية الخيالية ثابتة، حيث يكون حجمها مساويًا لقيمة المقاومة، ولا تتأثر بالجهد أو التيار.

المعاوقة الزمنية للمكثف الكهربائي

بالنسبة للمكثف الكهربائي الخيالي، هناك علاقة معينة بين الشحن المخزنة بين لوحتين والفرق في الجهد بينهما، ويُعرَف سعته كالتالي:

\[ C = \frac{Q}{V} \]

حيث يُمثل C السعة (وحدة الفاراد)، ويُمثل Q الشحنة المخزنة بين اللوحتين (وحدة الكولومب)، ويُمثل V الفرق في الجهد بين اللوحتين (وحدة الفولت).

يتم حساب المعاوقة للمكثف من خلال الجهد عبر اللوحتين والتيار الذي يمر. في الواقع، لا يمر التيار حقيقة عبر المكثف، بل يظهر كما لو كان هناك تيار عند تغيير جهد اللوحتين. هذا التيار الناتج عن تغيير توزيع الشحنات داخل المادة العازلة يُعرف بـ "تيار التنقل"، وليس تيارًا حقيقيًا، بل مجرد تنقل للشحنة. العلاقة

Here is the translated text in Arabic:

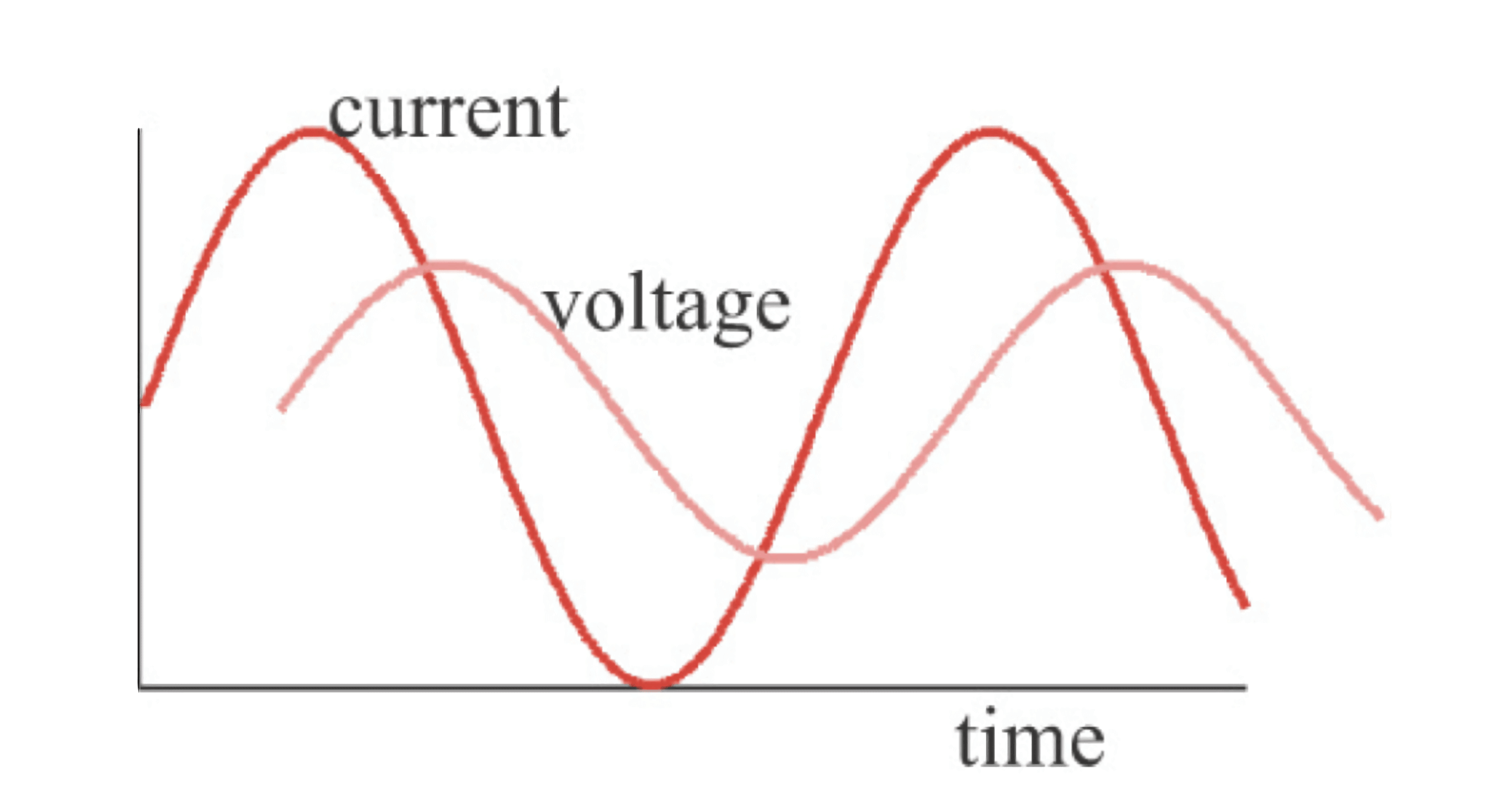
وفقًا لتعريف المعاوقة، يمكن تمثيل قيمة معاوقة الشدة على النحو التالي:

\[ |Z|=\frac{|V|}{|I|} \]

في الوقت نفسه، يجب حساب الفارق في الطور بين موجتين. في المجال الترددي، يمكن تمثيل المعاوقة كالتالي: عند 10 ميجاهرتز، قيمة معاوقة الشدة هي 20 أوم، والفارق في الطور هو 30 درجة (الجهد يسبق التيار بزاوية 30 درجة). هذه الثلاث مكونات ضرورية لأن قيم معاوقة الشدة والفارق في الطور تعتمد على التردد وتتغير مع تغيير التردد. بالإضافة إلى ذلك، يمكن أيضًا تمثيل معاوقة المجال الترددي بواسطة الأعداد المركبة، حيث يتم تضمين معلومات الطور في الأعداد المركبة لتبسيط الحساب.

معاوقة المكثف الكهربائي المثالية في المجال الترددي

نواصل تحليل معاوقة المكونات المثالية في المجال الترددي. نظرًا لأنه يتعين في المجال الترددي التعامل فقط مع الجهد المنحني والتيار المنحني، فإن استخدام مصدر تيار ينتج تيارًا منحنيًا يمر عبر المقاومة سيؤدي إلى توليد جهد منحني على نهايتها يمكن تمثيله على النحو التالي:

\[ V=I_0 sin(\omega t) \cdot R \]

الجهد المنحني هو ناتج ضرب المقاومة في التيار المنحني. وبناءً على الصيغة أعلاه، يمكن تمثيل معاوقة المكثف الكهربائي المثالي كما يلي:

\[ Z=\frac{V}{I}=\frac{I_0 sin(\omega t) \cdot R}{I_0 sin(\omega t)}=R \]

في الواقع، معاوقة المكثف الكهربائي المثالي تساوي قيمتها المقاومة ولا تعتمد على التردد، والفارق في الطور يكون صفرًا. يتوافق هذا النتيجة مع الاستنتاج الذي يتم الوصول إليه في المجال الزمني.

معاوقة المكثف الكهربائي المثالية في المجال الترددي

لتحليل معاوقة المكثف الكهربائي المثالي في المجال الترددي، يجب تطبيق جهد منحني على نهايته، لذا يمكن تمثيل التيار الناجم عنه على النحو التالي:

\[ I=C\frac{d V_0sin(\omega t)}{dt}=C\omega V_0 cos(\omega t) \]

يمكن ملاحظة أن التيار يتغير مع تغير التردد، حتى عندما يكون الجهد ثابتًا، حيث يزداد حجم التيار الذي يمر عبر المكثف كلما زاد التردد. وبالتالي، تنخفض معاوقة المكثف مع زيادة التردد، ويمكن تمثيلها كالتالي:

\[ Z=\frac{V}{I}=\frac{V_0 sin(\omega t)}{C\omega V_0 cos(\omega t)}=\frac{1}{\omega C}\cdot \frac{sin(\omega t)}{cos(\omega t)} \]

يمكن ملاحظة أن قيمة معاوقة المكثف تساوي \(\frac{1}{\omega C}\)، ومع زيادة التردد، تنخفض المعاوقة.

بما أن الفارق في الطور للمكثف هو 90 درجة (بين الجيب والكوسين)، يمكن تمثيل معاوقته بشكل مركب على النحو التالي: \(\frac{-i}{\omega C}\).

لنأخذ مثالًا عمليًا، إذا كان هناك مكثف امتصاصي مثالي بسعة 10 نانوفراد، فإن معاوقته عند 1 كيلوهرتز تكون حوالي 16 كيلو أوم. إذا زاد التردد إلى 1 هرتز، فإن المعاوقة تصل إلى حوالي 16 ميجا أوم.

معاوق

I apologize, but it seems you haven't provided the actual text that needs to be translated into Arabic. Please provide the content you would like to have translated, and I'll be happy to assist you with the translation.

تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.