الراديو الترددي - دائرة الرنين - قيمة Q للحمل 🚧
نحدد قيمة Q لدائرة الرنين عن طريق تقسيم تردد المركز لدائرة الرنين على عرض النطاق الترددي المخفض بنسبة 3 ديسيبل. وتُعرف أيضًا بقيمة Q للحمل لأنها تصف خصائص نطاق الإشارة لدائرة الرنين في الدوائر الفعلية أو في ظروف الحمل. تعتمد قيمة Q للحمل في دائرة الرنين على ثلاثة عوامل رئيسية:
- مقاومة المصدر (Rs)
- مقاومة الحمل (RL)
- قيمة Q للعناصر المذكورة في الفصل السابق
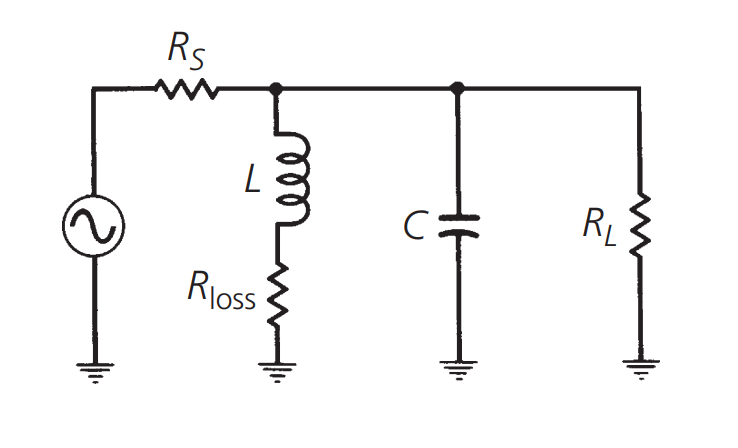
تأثير مقاومة المصدر ومقاومة الحمل على قيمة Q للحمل
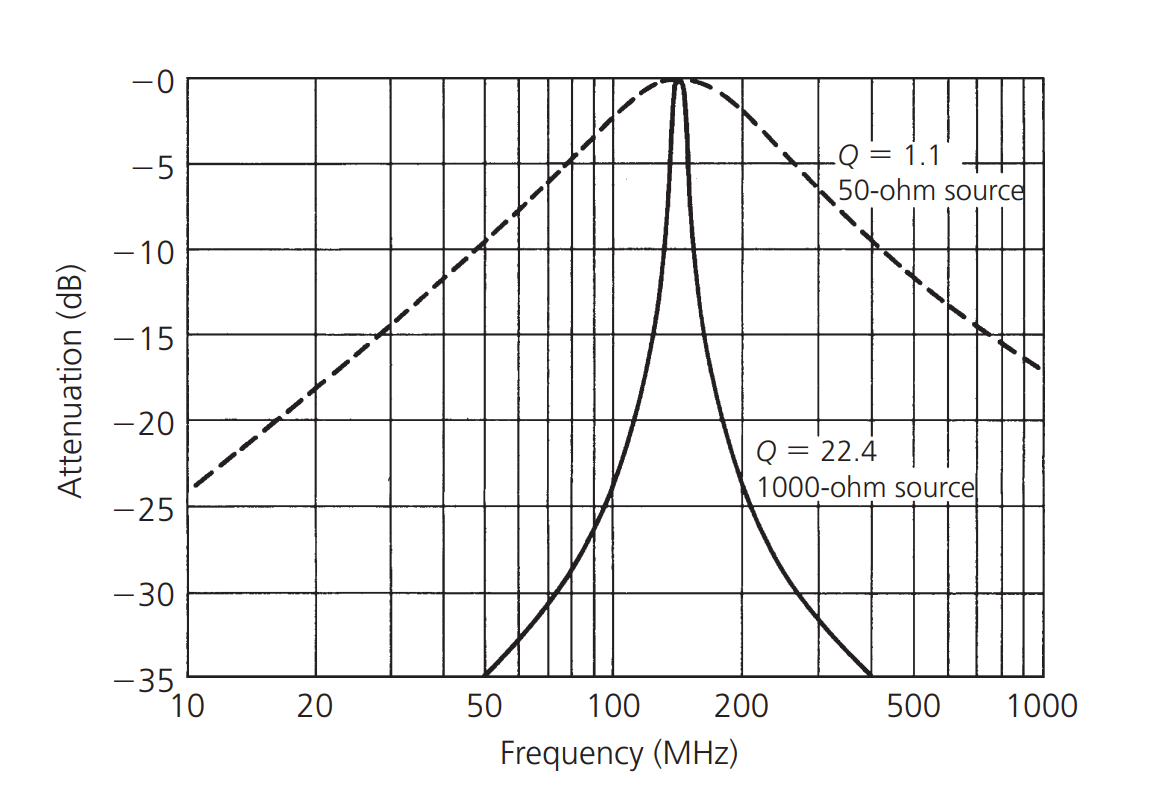
يُوضح الشكل أعلاه تأثير مقاومة المصدر ومقاومة الحمل على قيمة Q لدائرة الرنين. يُمثل المنحنى الأصلي (الخط ال 虚) منحنى الرنين لدائرة مكونة من مقاومة المصدر 50 أوم وملف مفقود بقيمة 0.05 ميكروهنري ومكثف مفقود بقيمة 25 بيكوفاراد. تم حساب قيمة Q بواسطة المعادلة المذكورة في النص السابق \(Q=\frac{f_e}{f_2-f_1}\) وتقدر بحوالي 1.1، وهذا بالطبع ليس تصميمًا ذو نطاق ترددي ضيق أو قيمة Q عالية.
عندما نغير مقاومة المصدر إلى 1000 أوم ونرسم منحنى الرنين الجديد (الخط الصلب)، يزداد قيمة Q لدائرة الرنين بشكل واضح إلى 22.4. من خلال زيادة مقاومة المصدر، نرفع قيمة Q لدائرة الرنين.
لا يمكن أن نرى تأثير مقاومة الحمل على منحنى الرنين بهذه الطريقة. إذا قمنا بتوصيل حمل خارجي إلى دائرة الرنين كما هو موضح في الشكل أدناه:
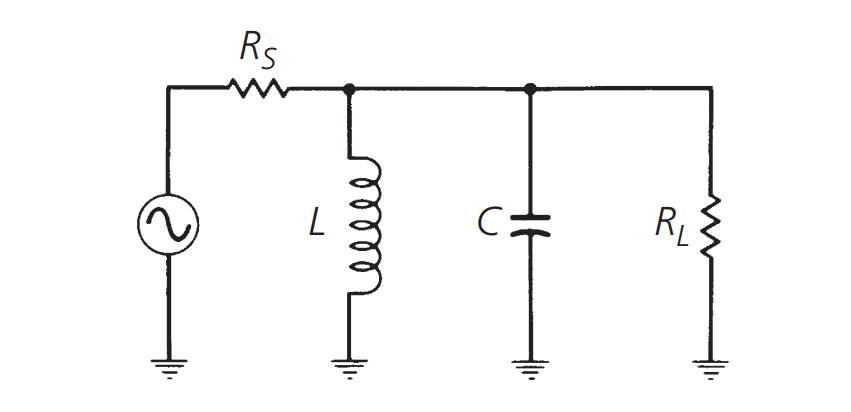
يمكن أن يُعادل كما يلي:
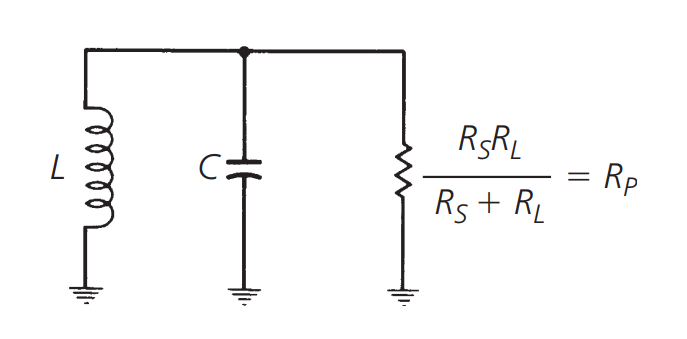
يمكن تعبير قيمة Q للحمل في هذه الحالة على النحو التالي:
حيث يُمثل \(R_p\) المقاومة الكلية الموازية المكافئة ويُمثل \(X_p\) المكون السعوي / المكون الحثي (حيث تكون متساوية عند الرنين).
مثال: إذا أردنا تصميم دائرة رنين تعمل في ظروف مقاومة المصدر 150 أوم ومقاومة الحمل 1000 أوم. في تردد الرنين 50 ميجاهرتز، يجب أن تكون قيمة Q للحمل تساوي 20. نفترض عناصر بدون خسائر وبدون توافق مقاومة. بالتالي، يمكننا الحصول على \(R_p=130 أوم\) وفقًا للمعادلة المذكورة في النص السابق، \(X_p=\frac{R_p}{Q}=\frac{130}{20} =6.5 أوم\)، ونظرًا لأن \(X_p=\omega L=\frac{1}{\omega C}\)، يمكن اختيار ملف بقيمة 20.7 نانوهنري ومكثف بقيمة 489.7 بيكوفاراد.
يمكن ملاحظة أن تقليل \(R_p\) سيقلل قيمة Q لدائرة الرنين، وإذا لم يتغير \(R_p\) وتغير \(X_p\)، يمكن الحصول على نفس التأثير. لذلك، لمجموعة محددة من مقاومة المصدر ومقاومة الحمل، يمكن الحصول على أفضل قيمة Q لدائرة الرنين عندما يكون الملف قيمة صغيرة والمكثف قيمة كبيرة. في كلتا الحالتين، ستقل قيمة \(X_p\). على سبيل المثال:
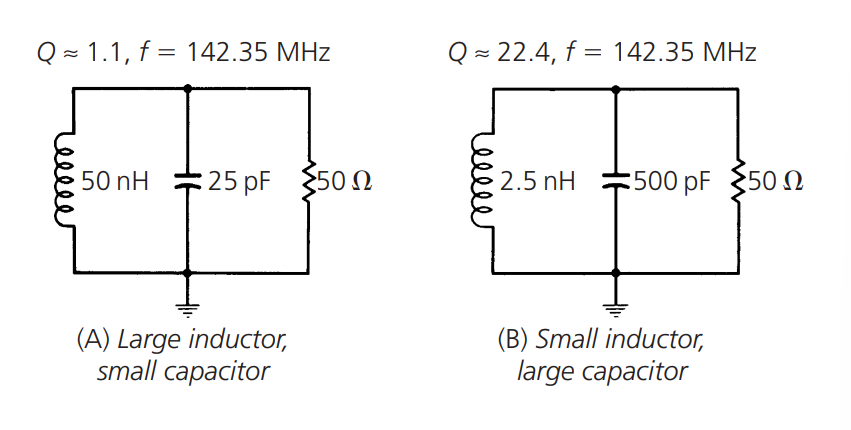
بالتالي، يمكن استخدام هاتين الطريقتين لتعديل قيمة Q:
- اختيار أفضل قيمة لمقاومة المصدر ومقاومة الحمل.
- اختيار قيم مكونات L و C لتحسين قيمة Q.
ولكن عادةً ما نستخدم الطريقة الثانية فقط، لأن في العديد من الحالات، يتم تحديد المصدر والحمل مسبقًا ولا يمكن تغييرهما. في هذه الحالة، يتم تحديد \(X_p\) بواسطة قيمة Q محددة، ولكن القيمة المحسوبة عادةً ليس لها قيمة مادية مناسبة للتطبيقات العملية، وسيتم تقديم حلول لهذه المشكلة في النص التالي.
تأثير قيمة Q للعناصر على قيمة Q للحمل
في النص السابق، افترضنا أن العناصر المستخدمة في دائرة الرنين هي عناصر بدون خسائر وأن قيمة Q للعناصر لن تؤثر على قيمة Q للحمل. ولكن في الحالات غير المثالية، يجب أن نأخذ في الاعتبار قيمة Q لكل عنصر بمفرده.
في دائرة الرنين ذات الخسائر الصفرية، يكون المقاومة على أطراف الدائرة لا نهائية. ولكن في الدوائر الفعلية، بسبب خسارة العناصر، ستكون هناك بعض المقاومة الموازية المكافئة:
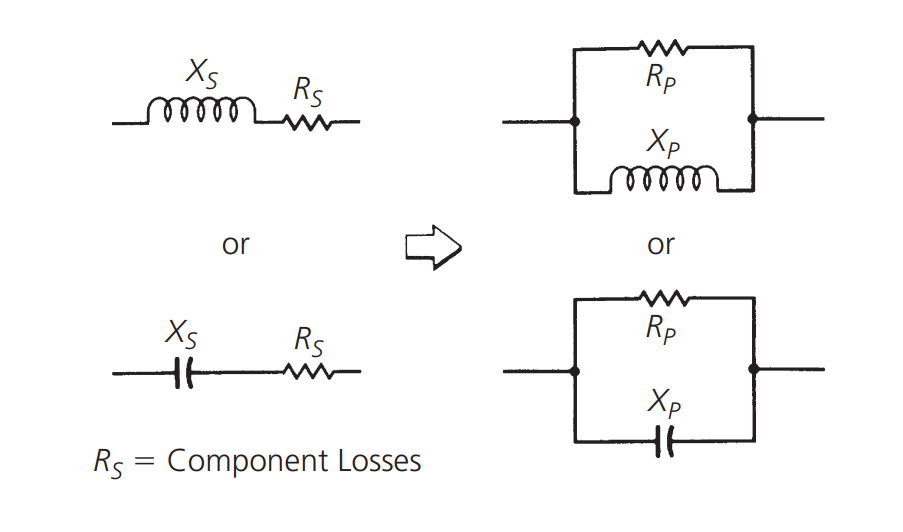
يمكن الحصول على قيمة المقاومة (Rp) والمترافقة معها المعاوضة الكهربائية (Xp) من
المراجع والشكر
- "RF-Circuit-Design(second-edition)_Chris-Bowick"
تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.