انتقل إلى المحتوى

ADC - المعلمات الثابتة

محول التناظري إلى رقمي (ADC) هو جهاز يحول الإشارات التناظرية إلى تسلسل من البيانات الرقمية.

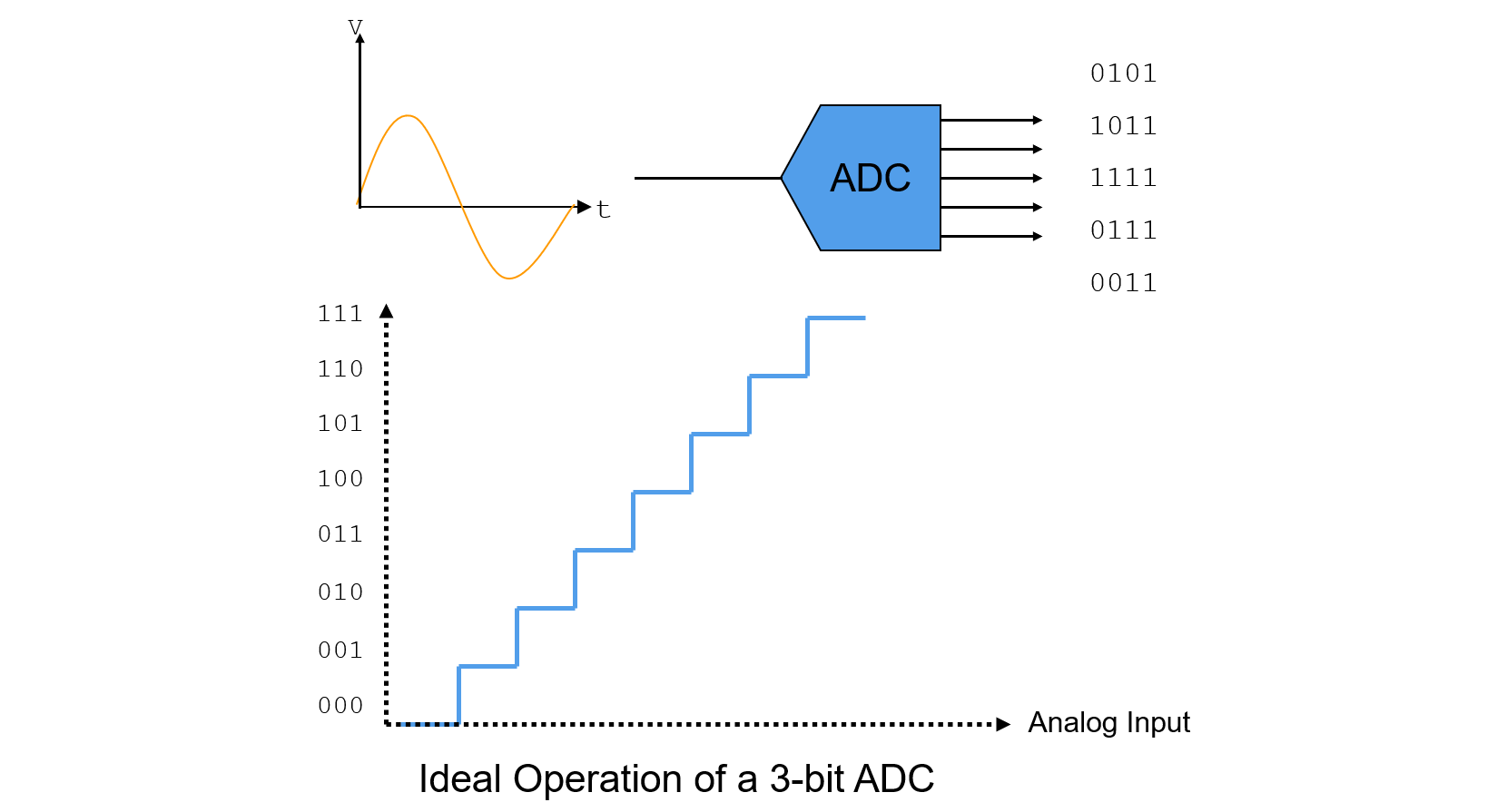
على الرغم من أن وظيفة نقل ADC المثالية يجب أن تكون خط مستقيم، إلا أنها في الواقع تشبه سلمًا متجانسًا، حيث يتوافق عدد الخطوات مع عدد أكواد الإخراج الرقمية. نظرًا لأن الإشارة التناظرية مستمرة والإشارة الرقمية م diskreta، سيتم إدخال خطأ التكميم في الإجراء.

المعلمات الثابتة

تحتوي المعلمات الثابتة لـ ADC بشكل رئيسي على:

  • حجم LSB
  • نطاق القيمة الكاملة (FSR)
  • خطأ الإزاحة
  • خطأ الكسب
  • خطأ عدم الخطية التفاضلية (DNE أو DNL)
  • خطأ عدم الخطية التكاملية (INE أو INL)

حجم LSB

يتم تعريف عرض خطوة واحدة كـ 1 أدنى بت معنوي (LSB). يتم تعبير دقة ADC عادةً بعدد البتات (رمز الإخراج الرقمي). يحتوي ADC بدقة n بت على \(2^n\) رمز رقمي ممكن (\(2^n\) مستوى خطوة).

\[ LSB=\frac{V_{FST}-V_{ZST}}{2^{bits}-2} \]

بالنسبة لـ ADC المثالي، يمثل LSB عرض كل رمز.

نطاق القيمة الكاملة (FSR)

على سبيل المثال، لمحول بت 3، هناك:

  • 8 خطوات أفقية
  • 7 انتقالات
  • 6 خطوات بين 7 انتقالات

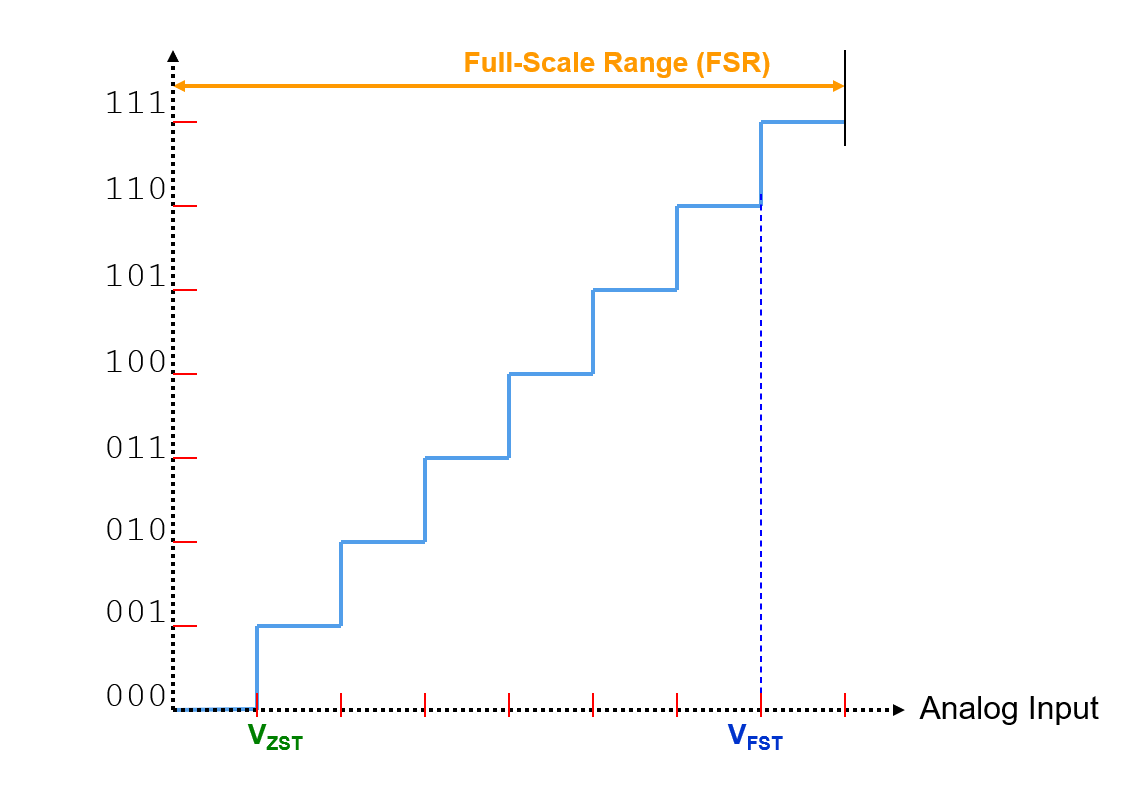
  • جهد انتقال نطاق الصفر (\(V_{ZST}\)): جهد إشارة الإدخال التناظرية عند تسجيل أول انتقال.
  • جهد انتقال نطاق القيمة الكاملة (\(V_{FST}\)): جهد إشارة الإدخال التناظرية عند تسجيل آخر انتقال.
  • نطاق القيمة الكاملة (FSR): الحد الأقصى للإشارة الإدخال التناظرية المزودة لـ ADC. \(FSR = (V_{FST}-V_{ZST}) + 2 LSB\)، \(V_{FSR(refer to VZS)} = (V_{FST}-0.5LSB)-(V_{ZST}-0.5LSB) + 2 LSB\)

خطأ الإزاحة

خطأ الإزاحة (خطأ الصفر) هو الفرق بين النقاط المثالية والفعلية للإزاحة (النقاط الأولية). يتم قياسه من منتصف الخطوة الصفرية (من المثالي إلى الفعلي) لمحول التناظر الرقمي إلى تمثيل رقمي.

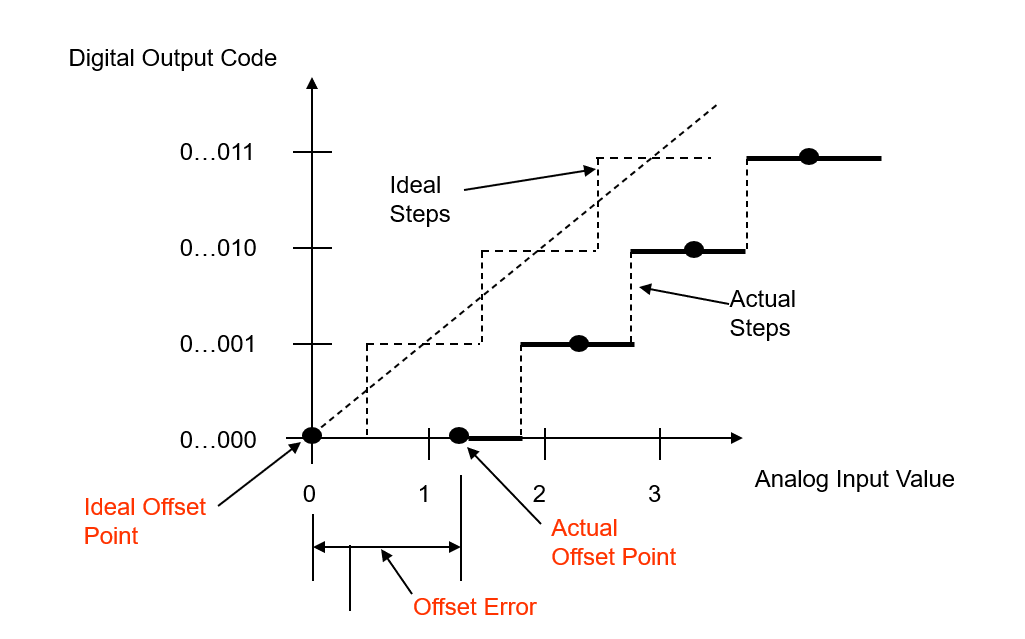
حيث

\[ V_{ZS}=V_{ZST}-0.5LSB \]

خطأ الكسب

خطأ الكسب هو الفرق بين النقاط المثالية والفعلية لنقاط الكسب على وظيفة الانتقال (بعد أن تم تصحيح خطأ الإزاحة ليصبح صفرًا). يتم قياسه من منتصف الخطوة الكاملة لمحول التناظر الرقمي إلى تمثيل رقمي.

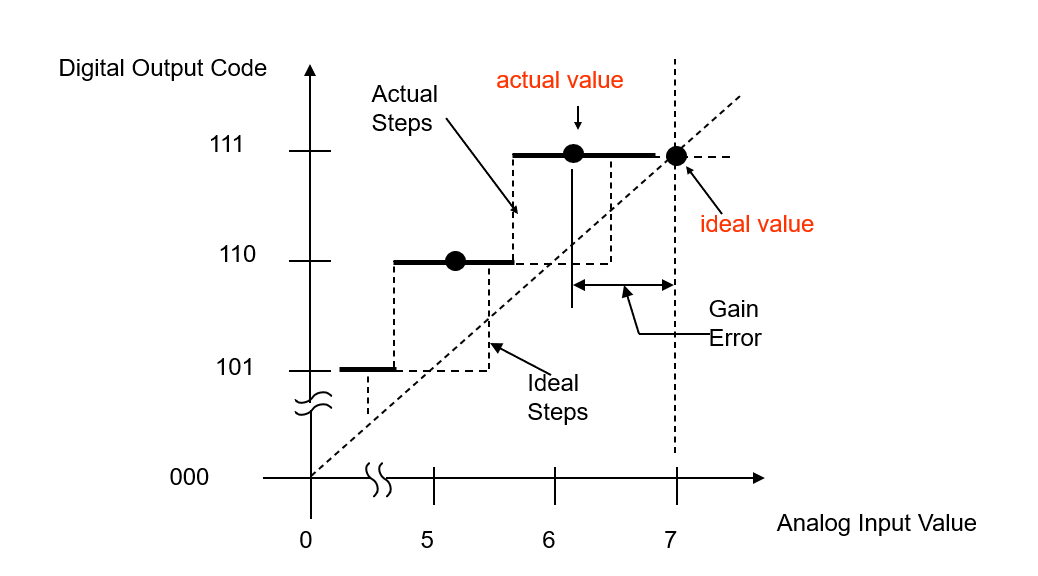
حيث

\[ V_{FS}=V_{FST}-0.5LSB+2LSB \]

خطأ عدم الخطية التفاضلي (DNL)

خطأ عدم الخطية التفاضلي (DNL) هو الفرق بين عرض الخطوة الفعلي وعرض الخطوة المثالي (1 LSB). إنها قياس لخطأ الخطية "الإشارة الصغيرة" ويتم قياسه من الفرق في جهد الإشارة التناظرية بين انتقالين متجاورين والقيمة المتوسطة لـ LSB للجهاز.

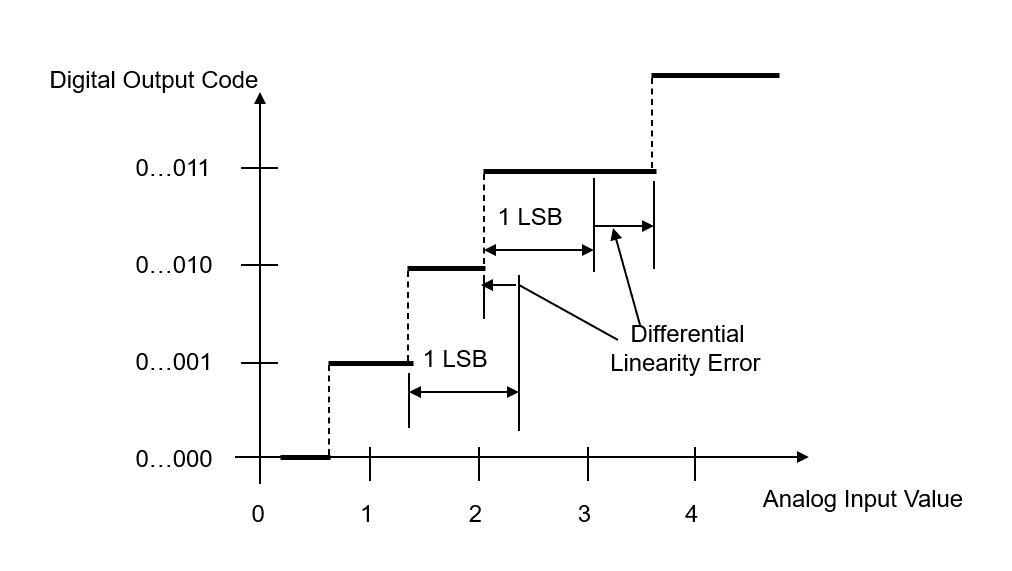
المعادلات التي تصف DNL:

\[ DNL[n]=CodeWidth_n-LSB_{average} \]
\[ DNL=(V_{in2}-V_{in1})-LSB_{average} \]

صورة أخرى لوصف DNL:

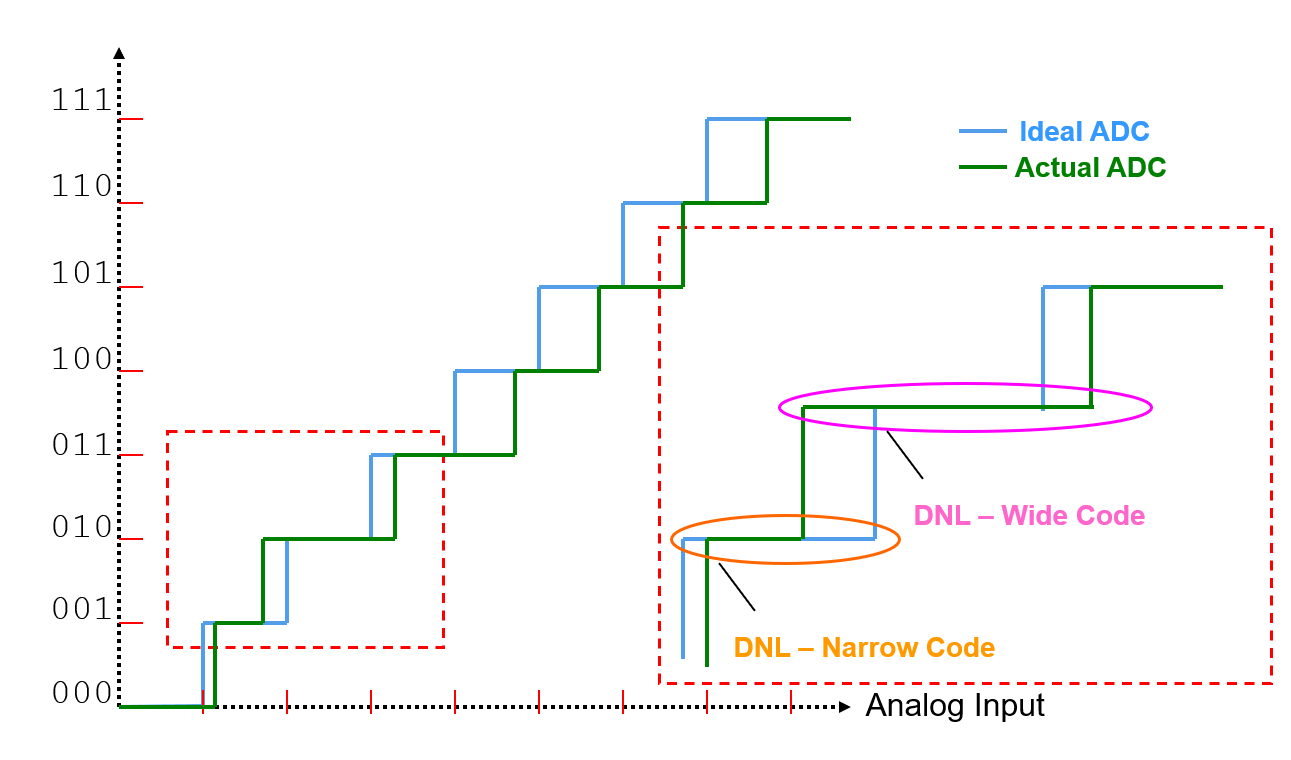
إذا تجاوز DNL الحد الأقصى، فإن واحدة أو أكثر من الرموز ستفقد ولن تحصل على إخراج.

خطأ عدم الخطية التكاملي (INL)

خطأ عدم الخطية التكاملي (INL) هو التأثير التراكمي في أي إشارة مدخل معين من جميع قيم عدم الخطية التفاضلية. إنها قياس لخطأ الخطية "الإشارة الكبيرة" ويعتبر INL في أي نقطة على الانحناءة هو انحراف الخط المثالي للخطية.

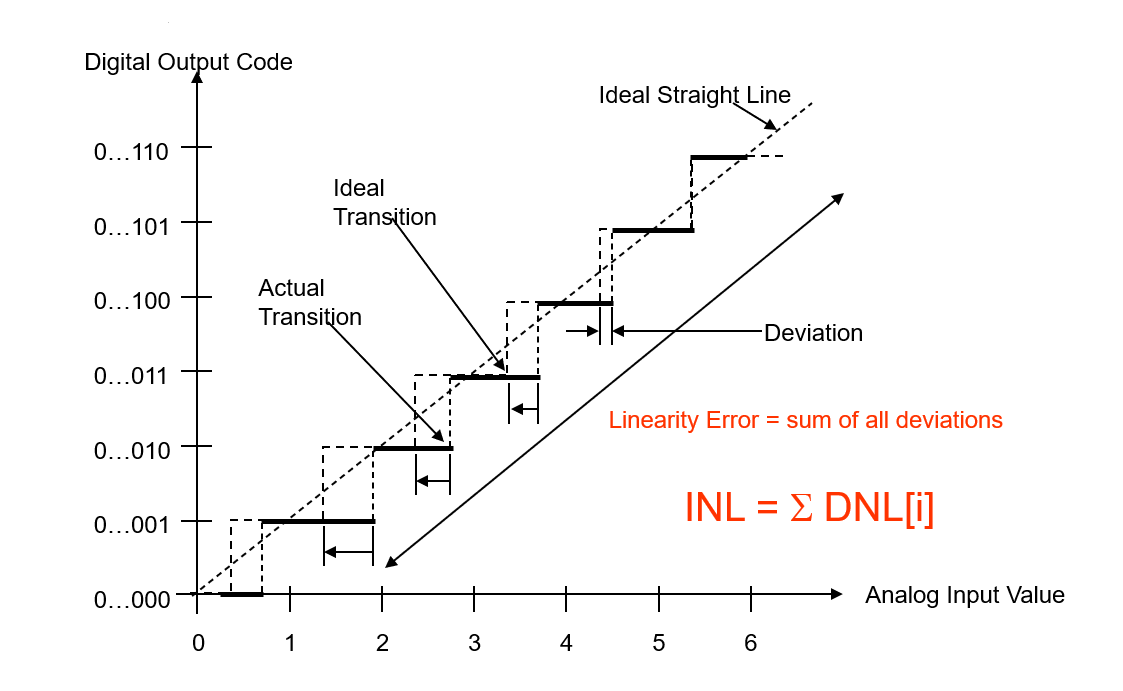
يتم قياس الانحرافات في نقاط الانتقال من خطوة واحدة إلى الأخرى لمحول التناظر إلى رقم. يعتبر INL هو الانحراف بين قيم الدالة الفعلية للخطوة والدالة المستقيمة المثالية.

المعادلات لوصف INL:

\[ INL[n]=INL_{n-1}+{\frac{DNL_{n-1}+DNL_{n}}{2}} \]
\[ INL=[(\frac{BinaryCode}{2^{bits}-1})(V_{FS}-V_{ZS})+V_{offset}]-CodeCentor \]

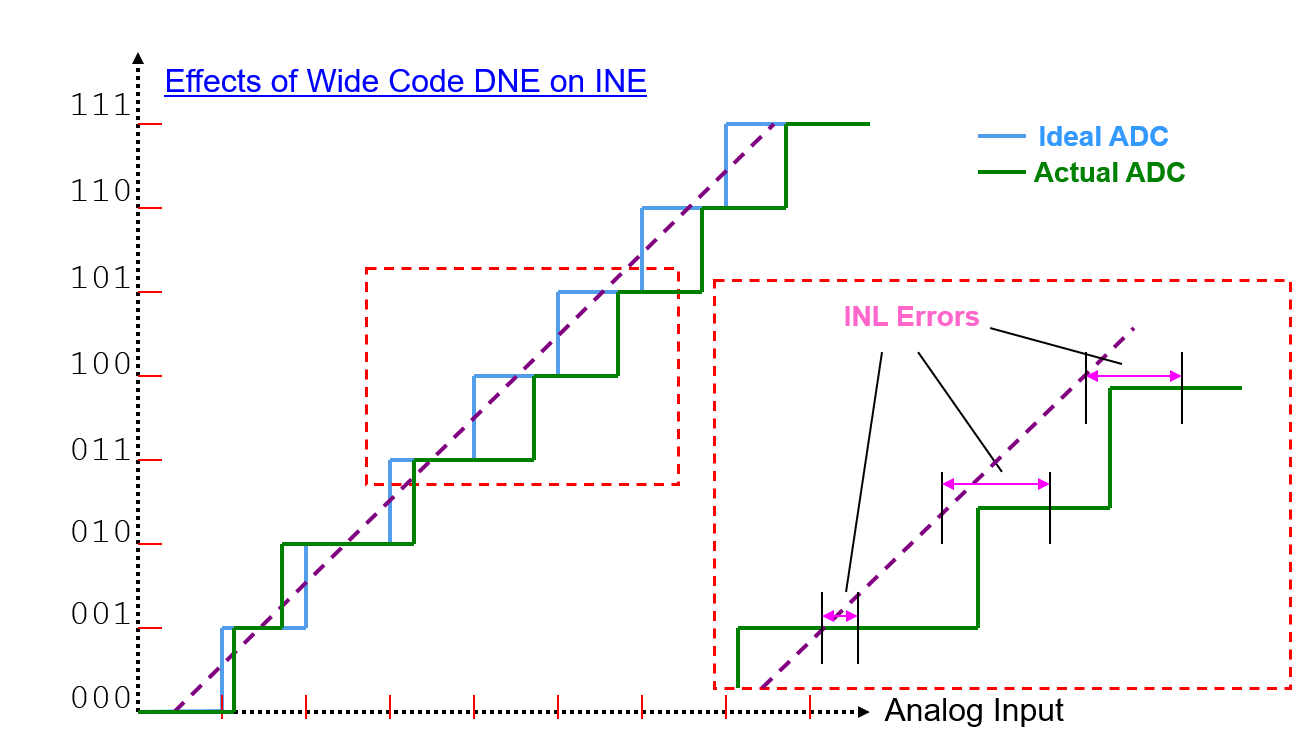
كيفية اختبار المعلمات الثابتة

إعداد نظام الاختبار

إعداد نظام الاختبار لاختبار المعلمات الثابتة لمحول التناظر إلى رقم:

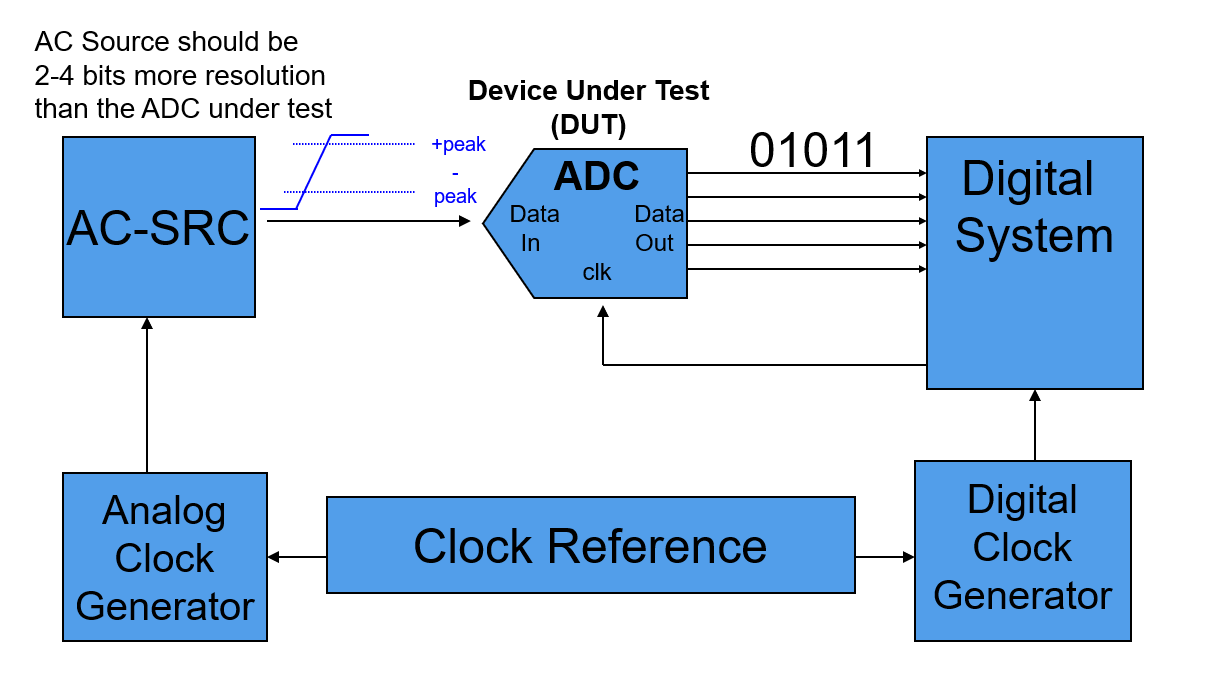
نظرًا لأن منحنى تحويل الجهد إلى رمز المحول التناظر إلى رقم هو وظيفة تعديل متعددة إلى واحدة:

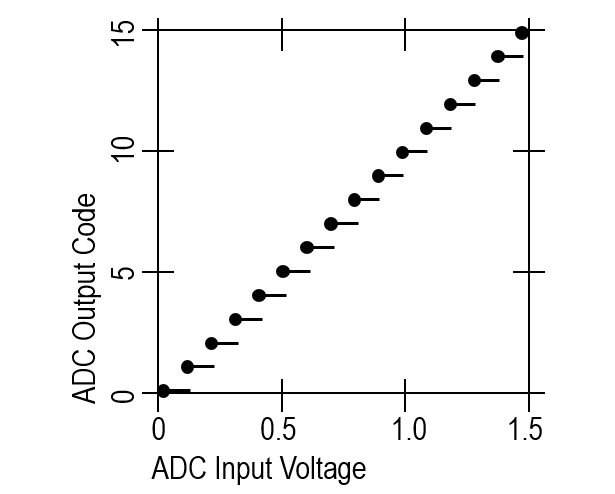
نستخدم في الواقع طريقة تصوير تدرج خطي (قياس عرض الرمز). يكون التدرج المدخل بطيئًا بما يكفي لتوفير "عدد مناسب إحصائيًا من الأكواد لكل رمز".

مخطط كتلة إعداد الإشارة:

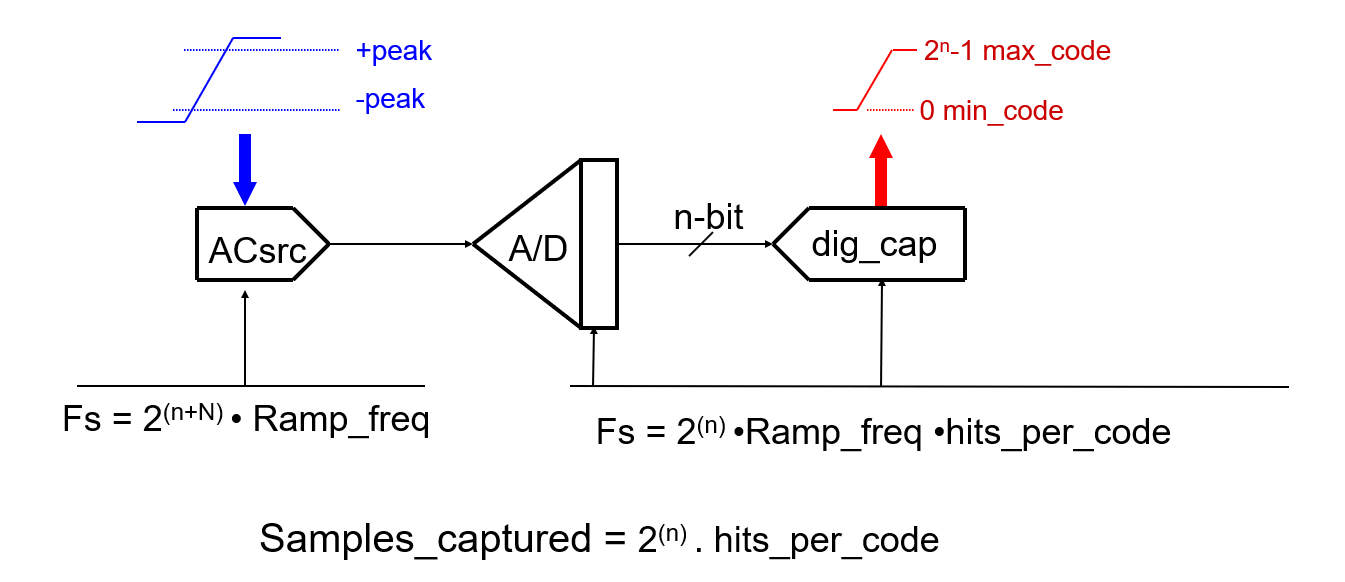
مفهوم الاختبارات

يتم سرد إجراء اختبار المعلمات الثابتة لجهاز اختبار ADC كما يلي.

1. إنشاء قطاع موجة تدرج لمصدر AC

يتجاوز التدرج المدخل القيمة المطلوبة أعلى وأدنى ±Fs لضمان تغطية جميع الأكواد:

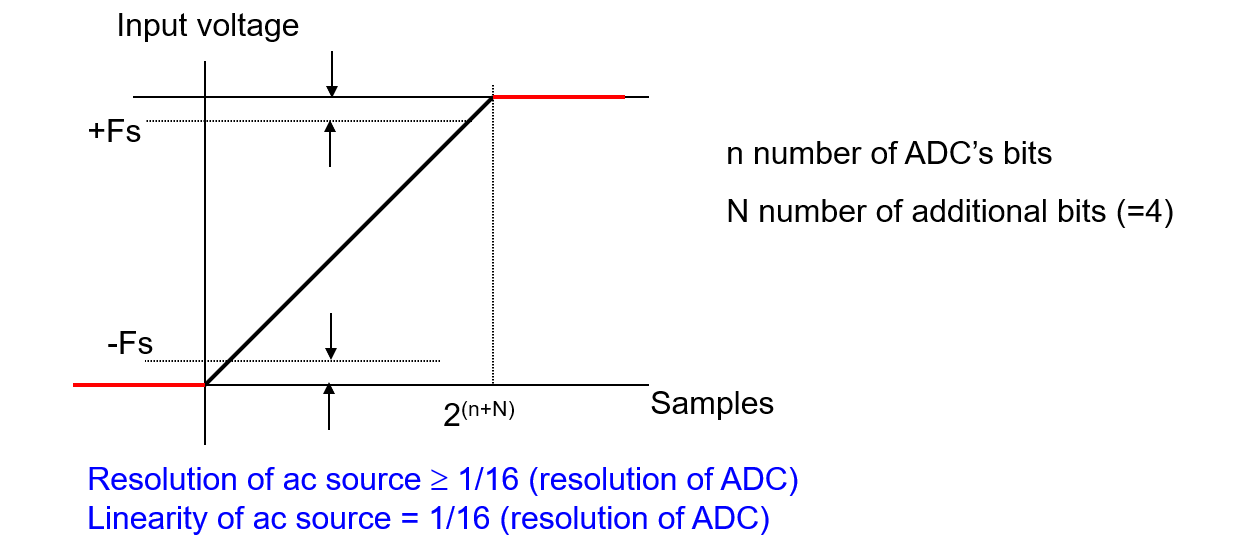
2. استخراج البيانات بين البداية (min+1، على سبيل المثال 0…01) والنهاية (max-1، على سبيل المثال 1…10) للتدرج. هذا يعطي قيمة بيانات تعادل \(2^n – 2\) للأكواد

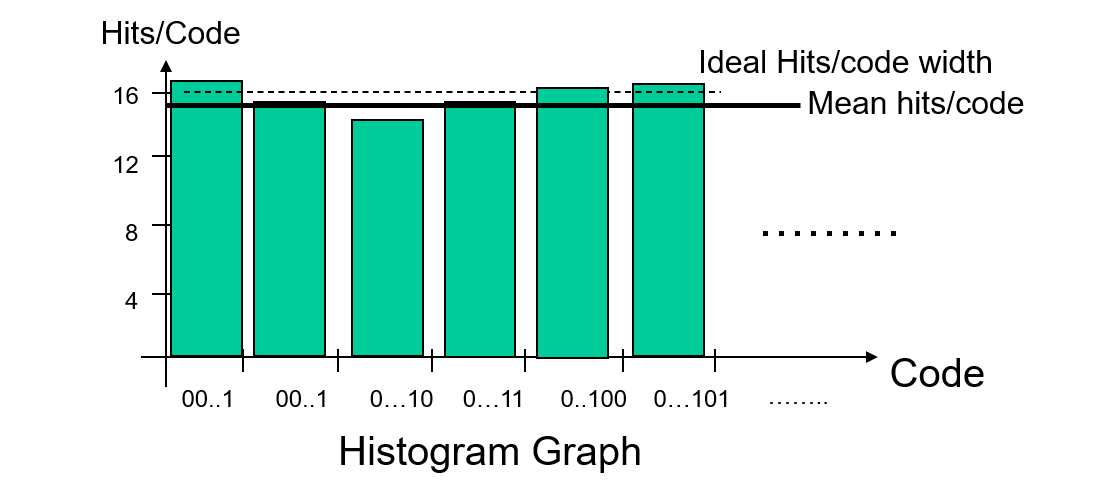
يجب أن يكون الجهد المطبق أوسع من نطاق القيمة القصوى لتغطية جميع الانتقالات. يتم عرض 16 خطوة بين كل انتقال للأكواد في الشكل أدناه:

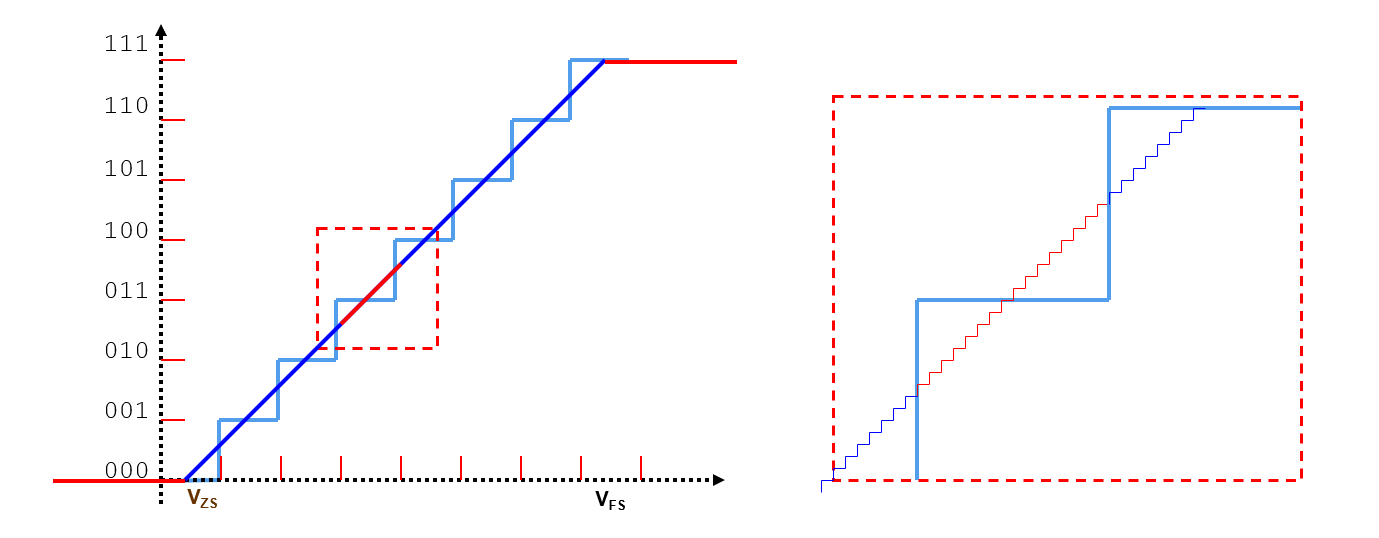
بالنسبة لجهاز اختبار ADC المثالي ، تظهر 16 أكواد إخراج في نفس الوقت:

ترجمة إلى العربية:

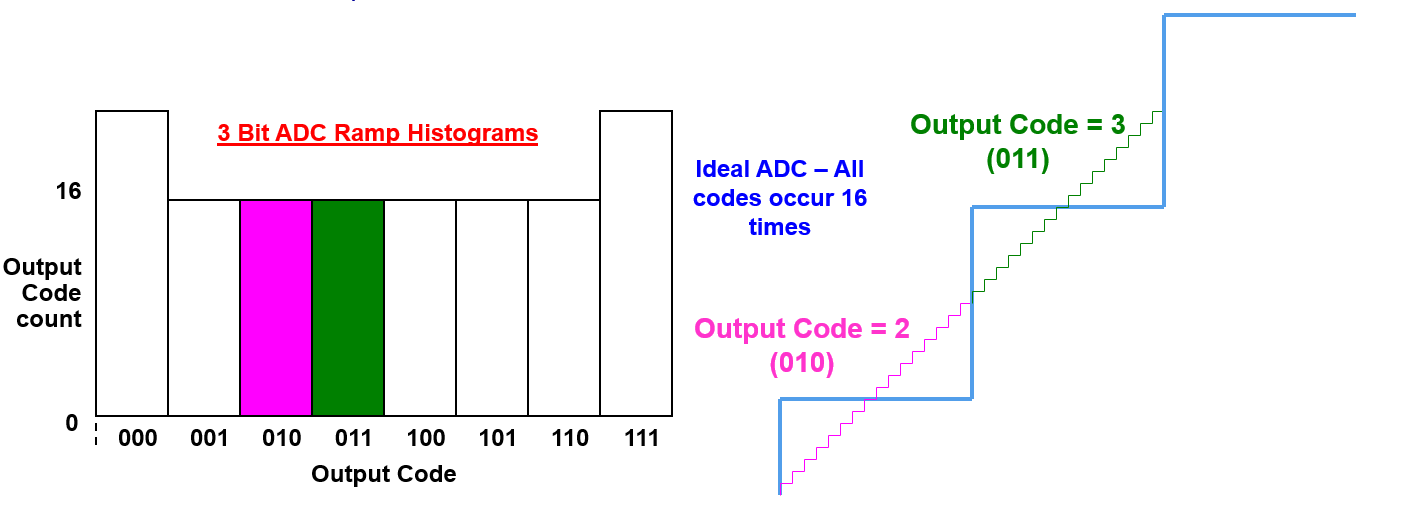
ومع ذلك، ستكون لدى الجهاز الفعلي عدد مرات أكثر بـ 16 مرة للأكواد الأوسع، وأقل من 16 مرة للأكواد الأضيقة (ولكن مجموع الحدوث الكلي يجب أن يكون لا يزال \(2^{bits}\) مرة من 16):

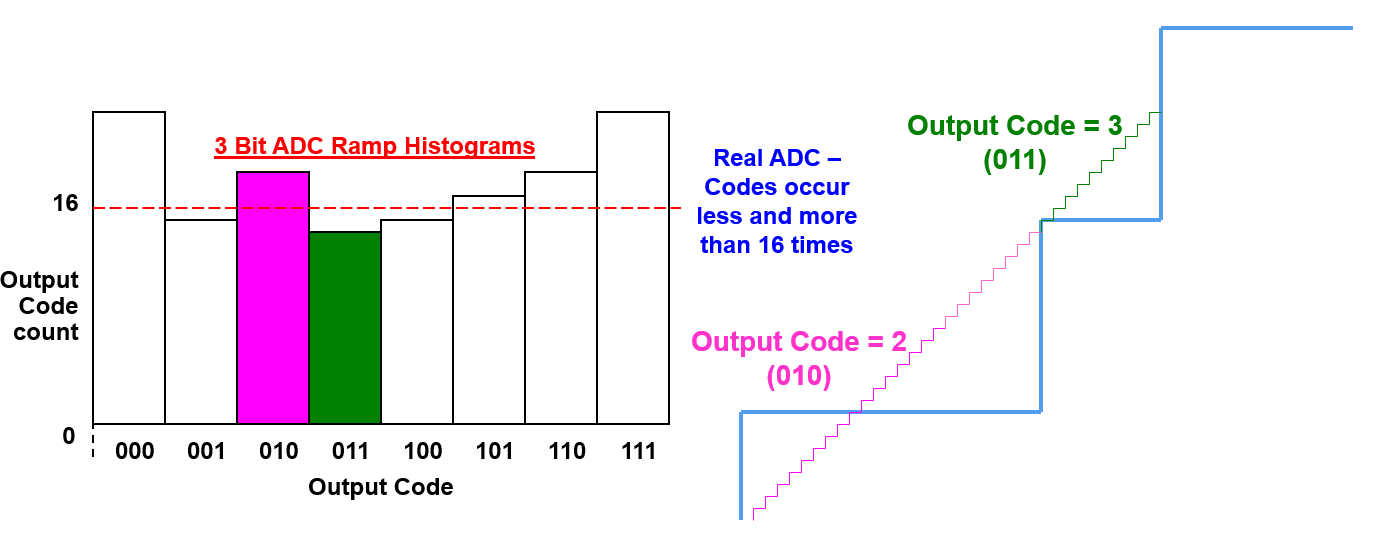
3. حساب DNL لكل خطوة

\[ DNL[i]=\frac{Hits[i]-\frac{\sum Hits[i]}{2^n-2}}{\frac{\sum Hits[i]}{2^n-2}} \]

حيث يمثل \(Hits[i]\) عدد أكواد الإخراج الفعلية، ويمثل \(\frac{\sum Hits[i]}{2^n-2}\) عدد أكواد الإخراج المثالية.

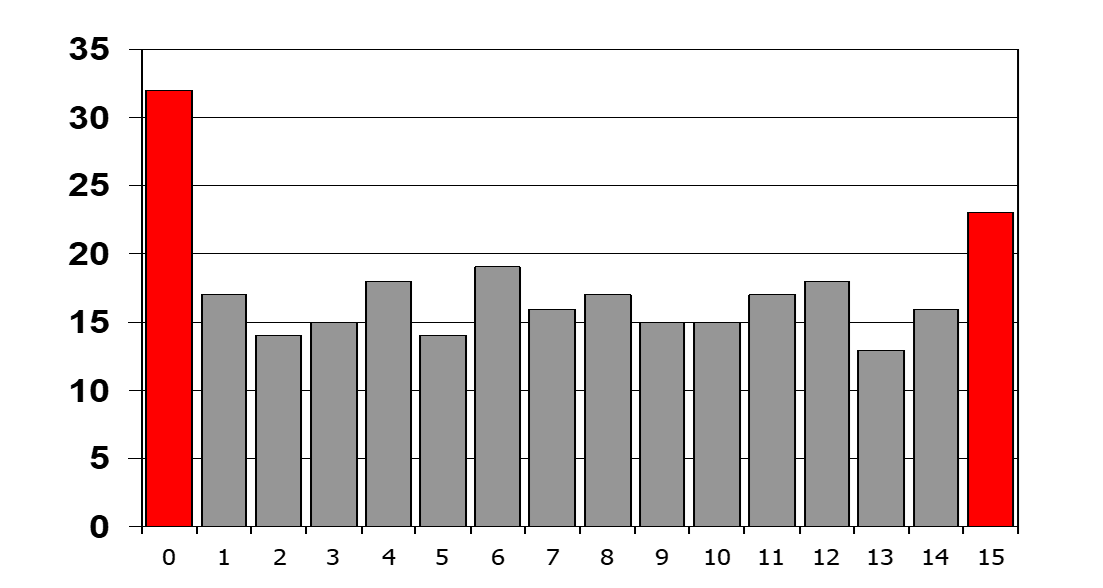
لمثال الرسم البياني للتوزيع كما هو موضح أدناه:

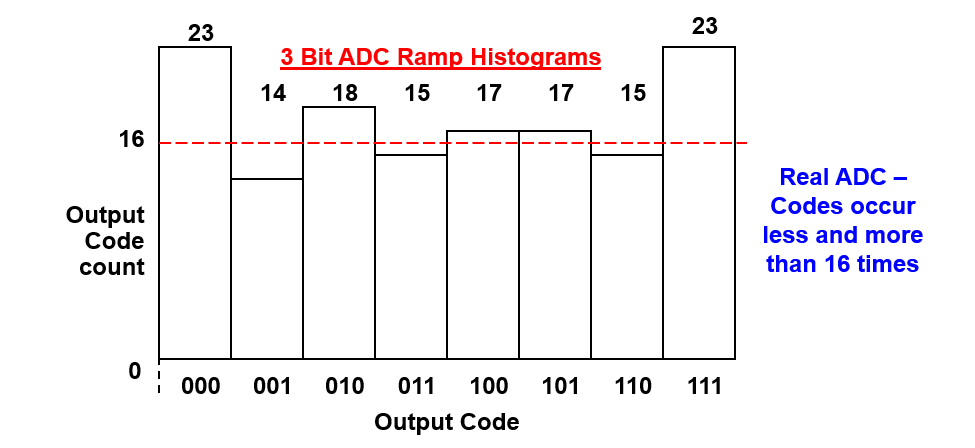
بالنسبة لـ \(DNL[1](Code 001)\)،

  • عدد أكواد الإخراج الفعلية = 14
  • عدد أكواد الإخراج المثالية = (14 +18 +15 + 17+ 17 + 15) / (8 -2 ) = 16.

لذلك \(DNL[1] (Code 001) = (14-16)/16 \ LSB => -0.125 \ LSB\).

4. الحصول على أقصى وأدنى DNL

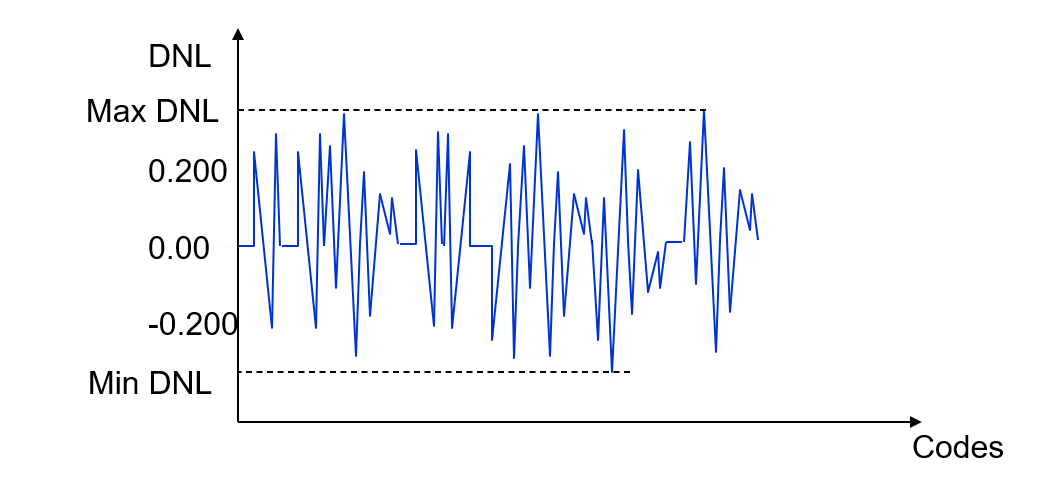
5. حساب INL لكل خطوة

INL هو القيمة التراكمية لأول DNL إلى DNL[i] (باستثناء DNL صفر و DNL مدى كامل):

\[ INL[i]=DNL[i]+DNL[i-1]+...+DNL[2]+DNL[1] \]

يرجى ملاحظة أنه لا يتم استخدام \(DNL[0]\)،

\[ INL[0]=INL[FullScale]=0 \]

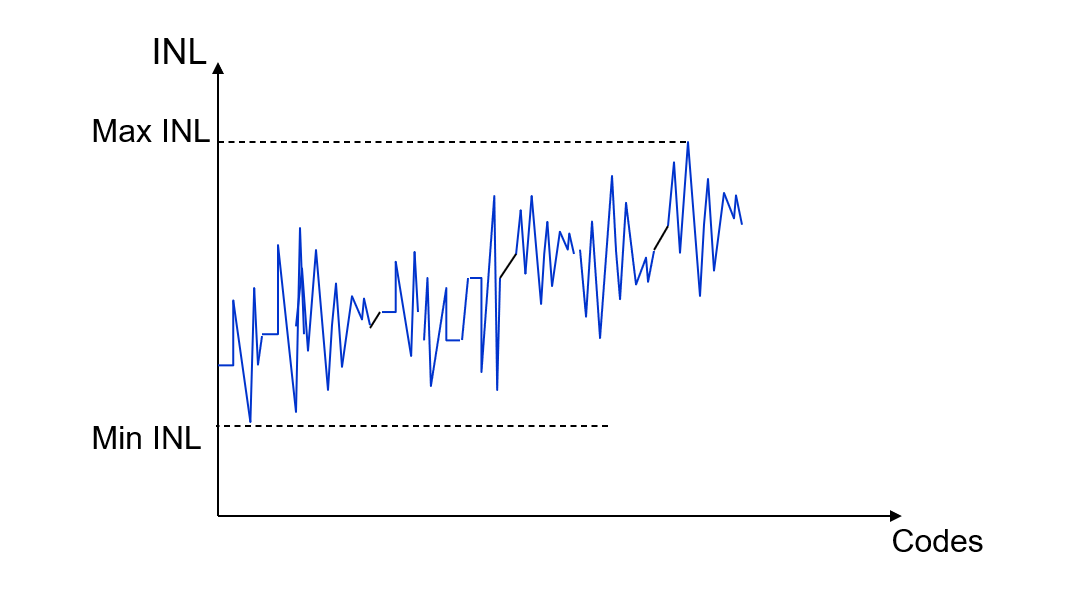
للرسم البياني الموضح أدناه،

\[ INL[1] = DNL[1] = -0.125 * LSB \]
\[ INL[2] = DNL[2] + DNL[1] = 0 * LSB \]
\[ INL[3] = DNL[3] + DNL[2] + DNL[1] \\ INL[3]= 0.0625 * LSB \]

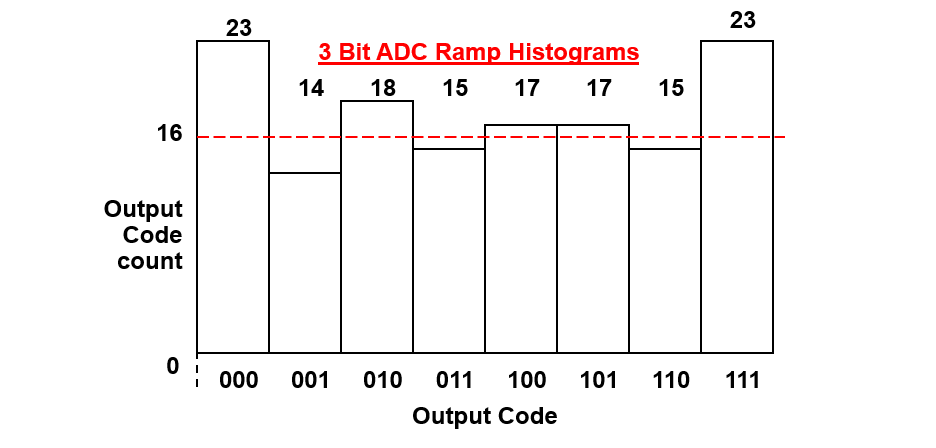
6. الحصول على أقصى وأدنى INL

المراجع والشكر

  • أساسيات الاختبار باستخدام ATE
  • The-Fundamentals-of-Mixed-Signal-Testing_Brian-Lowe

Original: https://wiki-power.com/
هذه المشاركة محمية بموجب اتفاقية CC BY-NC-SA 4.0، يجب إعادة إنتاجها مع الإشارة إلى المصدر.

تمت ترجمة هذه المشاركة باستخدام ChatGPT، يرجى تزويدنا بتعليقاتكم إذا كانت هناك أي حذف أو إهمال.