Integridad de la señal - Líneas de transmisión 🚧
Las líneas de transmisión son componentes ideales compuestos por dos conductores de longitud fija, conocidos como trayecto de la señal y trayecto de retorno (trayecto de referencia). Las líneas de transmisión poseen dos características fundamentales: la impedancia característica y la retardancia.
Modo de transmisión de la señal
Para comprender la transmisión de la señal, es necesario observar tanto el trayecto de la señal como el trayecto de retorno. ¿Cómo se determinan estos trayectos? Si los dos conductores son idénticos (por ejemplo, en cables de par trenzado), no existe una distinción estricta. Sin embargo, en el caso de cables microstrip, generalmente se especifica el plano como el trayecto de retorno. Es importante destacar que, en el contexto de la integridad de la señal, utilizamos el concepto de "trayecto de retorno" en lugar de simplemente "tierra" porque las situaciones que debemos analizar son mucho más complejas que una simple conexión a tierra.
Una vez que la señal entra en la línea de transmisión, se propaga a través del medio a la velocidad de la luz. Podemos representar la señal como la diferencia de voltaje entre dos puntos adyacentes en el trayecto de la señal y el trayecto de retorno:
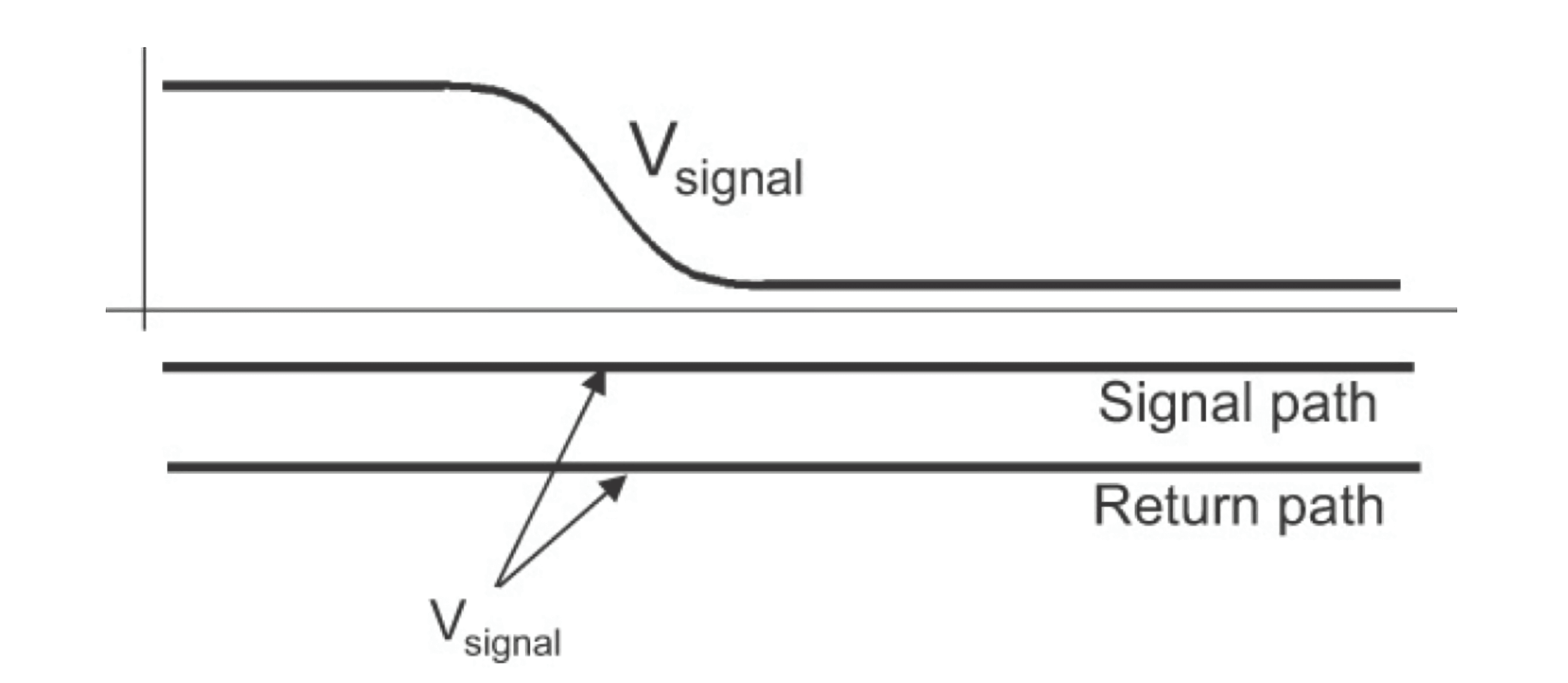
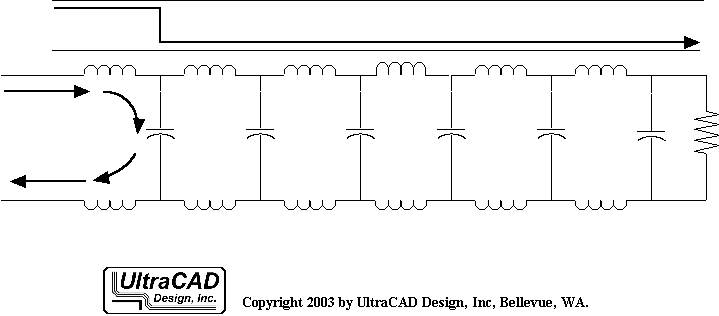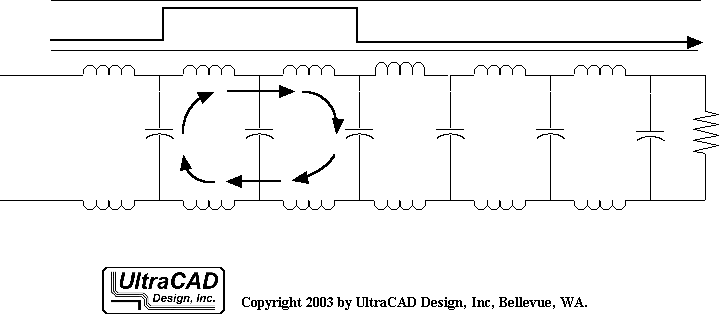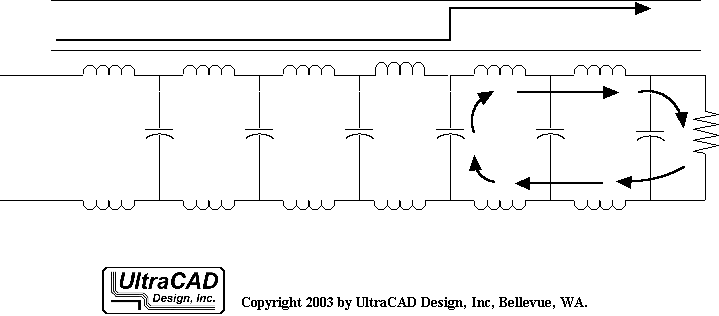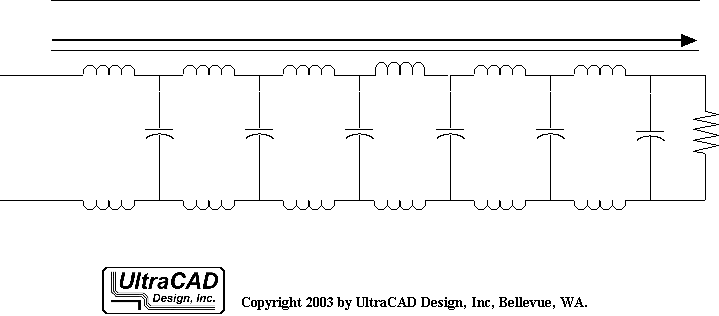
Si suponemos un par de líneas de transmisión lo suficientemente largas y abiertas en los extremos, con corrientes conectadas en el extremo de origen y en el extremo de destino, podemos detectar la corriente de la señal. En experimentos reales, observamos que cuando la señal ingresa al trayecto de la señal, ya hemos comenzado a detectar corriente en el trayecto de retorno. Por lo tanto, el circuito de corriente no se completa desde el extremo de origen hasta el extremo de destino y luego de vuelta por el trayecto de retorno. En cambio, la corriente se genera a medida que la señal avanza debido a la diferencia de potencial creada por la señal y el trayecto de retorno, similar a la carga de un condensador. A medida que la señal se propaga, el punto donde se genera la corriente se desplaza continuamente hacia adelante.
Líneas de transmisión uniformes y equilibradas
Cuando clasificamos las líneas de transmisión, podemos hacerlo en función de dos características: la uniformidad en la sección transversal a lo largo de la línea y la simetría entre los dos conductores.
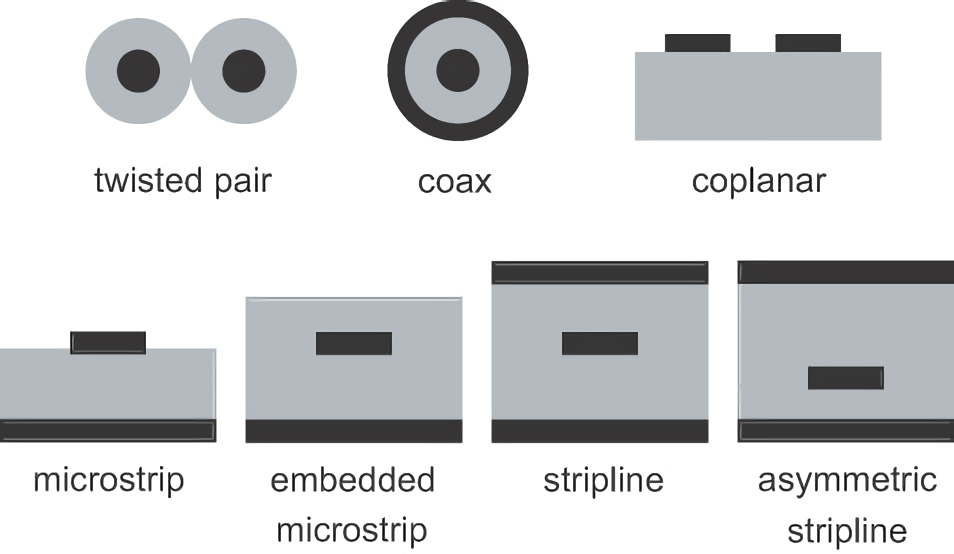
Si en cualquier punto a lo largo de los conductores la sección transversal es idéntica, se le llama línea de transmisión uniforme o línea de impedancia controlada. Ejemplos de esto son los cables de par trenzado y las líneas microstrip:
Un objetivo del diseño de la integridad de la señal es convertir todas las interconexiones de alta velocidad en líneas de transmisión uniformes y reducir al máximo la longitud de las líneas no uniformes.
Otra característica de clasificación se basa en la similitud/simetría de los dos conductores. Si ambos conductores tienen la misma forma y tamaño, se trata de una línea de transmisión equilibrada, como los cables de par trenzado. Por otro lado, un ejemplo de línea no equilibrada es el cable coaxial, donde el conductor central tiene una sección transversal más pequeña que el conductor exterior.
Velocidad de propagación de la señal
La velocidad de propagación de la señal en una línea de transmisión no depende de la velocidad de los electrones en el conductor.
Si conocemos la cantidad de electrones que pasan por la sección transversal del conductor por segundo, la densidad de electrones en el conductor y el área de la sección transversal del conductor, podemos calcular la velocidad de los electrones en el conductor. Esto se debe a que la corriente en el conductor (\(I\)) se puede calcular mediante la siguiente fórmula:
Donde \(\Delta Q\) representa la cantidad de carga que pasa a través del conductor en \(\Delta t\) (en Coulombs), \(q\) es la carga de un electrón libre y es una constante de \(1.6\times 10^{-19}C\), \(n\) es la densidad de electrones libres (en \(\#/m^3\)), y \(A\) es el área de la sección transversal del conductor (\(m^2\)). Por lo tanto, podemos calcular la velocidad de los electrones (\(m/s\)) de la siguiente manera:
En materiales comunes, la velocidad de movimiento de los electrones es muy baja. Por ejemplo, en un cable de cobre con un diámetro de 1 mm (la distancia entre los átomos de cobre es de aproximadamente 1 nm, y cada átomo de cobre proporciona dos electrones libres, lo que da una densidad de electrones libres de alrededor de \(10^{27}/m^3\)), cuando pasa una corriente de 1 A, la velocidad de los electrones es de aproximadamente 1 cm/s. Es evidente que la velocidad de los electrones es significativamente más lenta que la velocidad de propagación de la señal.
Además, la reducción de la resistencia de la interconexión no necesariamente aumenta la velocidad de propagación de la señal. Solo en situaciones extremas, la resistencia de la línea de interconexión afectará ligeramente la velocidad de propagación de la señal. En condiciones normales, una resistencia baja en el conductor no implica una velocidad de transmisión más rápida.
El principio de la transmisión de señales a través de electrones se basa en la interacción entre los electrones.
**Traducción al español:**
Puedes imaginar los conductores como un largo tubo lleno de canicas. Si empujas una canica en un extremo, casi al mismo tiempo, saldrá otra canica por el otro extremo. Aquí, la velocidad de transmisión de las canicas que llevan la señal es mucho más rápida que la velocidad real de movimiento de las canicas. De manera similar, cuando los electrones en un conductor son impulsados por electrones adyacentes, la velocidad de propagación de la señal no depende de la velocidad de movimiento de los electrones en sí, sino más bien de la interferencia entre ellos.
A medida que la señal se transmite, se genera un campo electromagnético alternante en el conductor entre la señal y el camino de retorno, así como en el espacio circundante al conductor. El factor que determina la velocidad de propagación de la señal es la velocidad de creación y propagación de este campo electromagnético.
La velocidad de cambio del campo electromagnético (velocidad de la cadena del campo) se puede calcular mediante la siguiente fórmula:
$$
v = \frac{1}{\sqrt{\varepsilon_0\varepsilon_r\mu_0\mu_r}}
$$
Donde $\varepsilon_0$ es la permitividad en el espacio libre y tiene un valor de $8.89\times 10^{-12} F/m$; $\varepsilon_r$ es la permitividad relativa del material y en el aire es igual a 1; $\mu_0$ es la permeabilidad en el espacio libre con un valor de $4\pi\times10^{-7} H/m$; y $\mu_r$ es la permeabilidad relativa del material, que es casi 1 para la mayoría de los dieléctricos de interconexión. Sustituyendo las constantes mencionadas en la fórmula, obtenemos:
$$
v = \frac{2.99\times 10^8}{\sqrt{\varepsilon_r}} m/s = \frac{12}{\sqrt{\varepsilon_r}} inch/ns
$$
Comparado con el aire, la permitividad $\varepsilon_r$ de otros materiales generalmente es mayor que 1, y la velocidad de la luz es de aproximadamente $12 inch/ns$. Por lo tanto, la velocidad real en la interconexión es menor que $12 inch/ns$, y se calcula como:
$$
v = \frac{12}{\sqrt{\mu_r}} inch/ns
$$
La permitividad relativa también se conoce comúnmente como permitividad. La mayoría de los polímeros tienen un valor alrededor de 4. Por lo general, la permitividad disminuye a medida que aumenta la frecuencia, pero en materiales de PCB comunes, la variación es pequeña. Por ejemplo, la permitividad del FR4 varía entre 3.5 y 4.5, mientras que los materiales de alta velocidad varían entre 3 y 4. Según la fórmula, la velocidad de la señal en el FR4 es aproximadamente de $6 inch/ns$ (sin considerar el efecto del campo electromagnético en el aire).
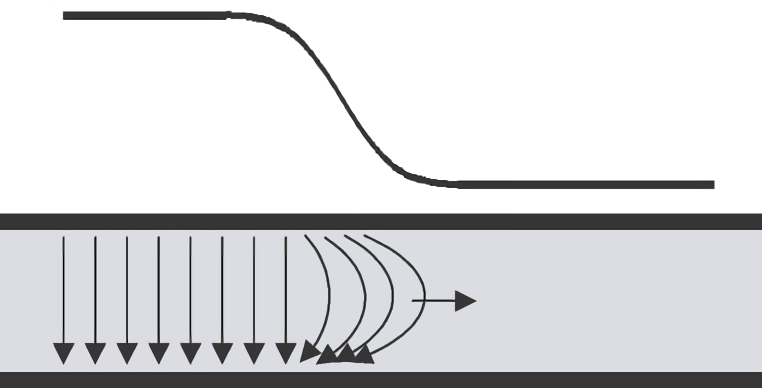
## Extensión espacial del frente
El flanco ascendente de una señal, RT, generalmente representa el tiempo que lleva cambiar del 10% al 90% del voltaje máximo. Cuando la señal se propaga por la línea de transmisión, adelanta este borde, creando una extensión espacial:
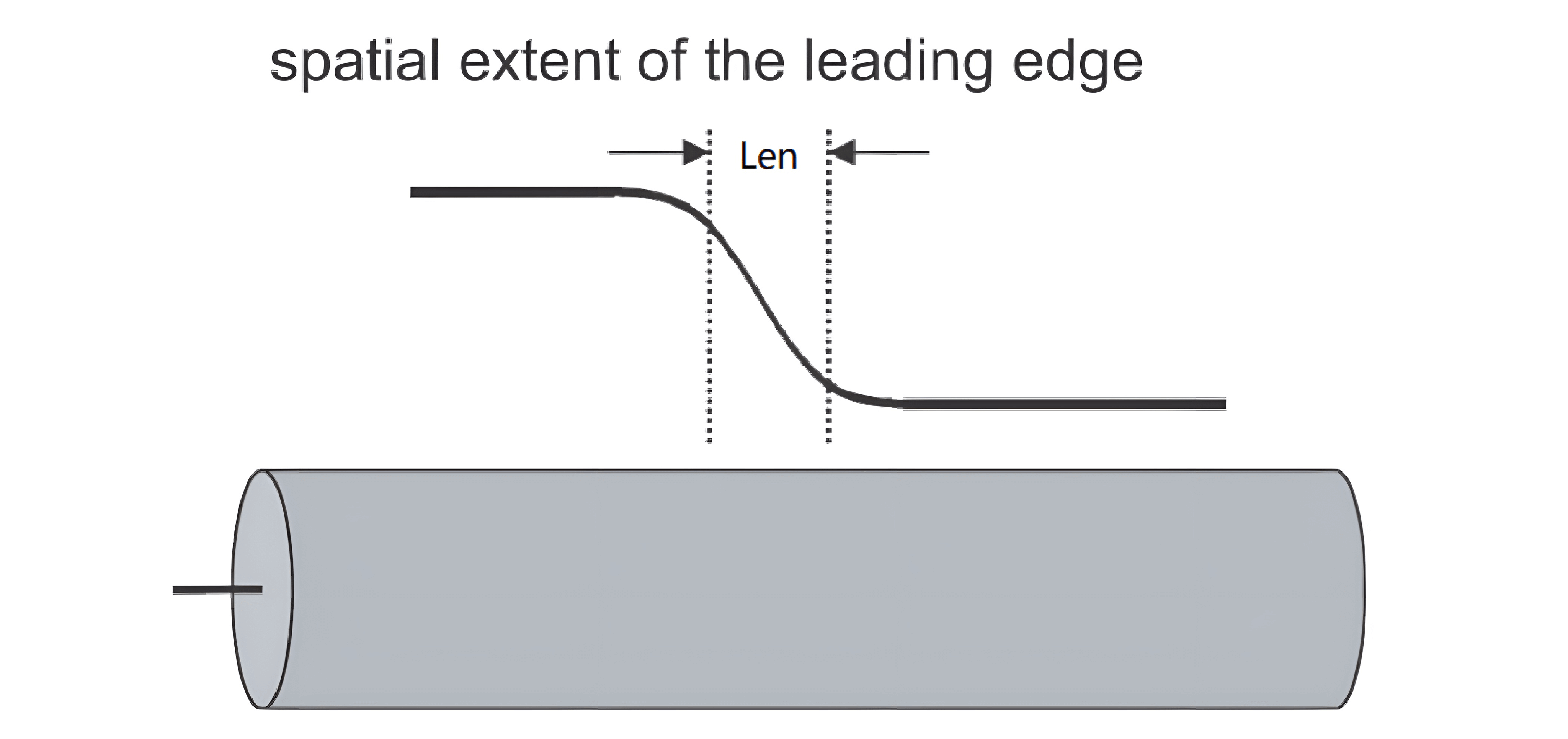
La longitud de esta extensión depende de la velocidad de la señal y la duración del flanco ascendente:
$$
Len = RT \times v
$$
Supongamos que la velocidad de la señal es de $6 inch/ns$ y la duración del flanco ascendente es de 1 ns, entonces la extensión espacial del frente es de 6 pulgadas. La señal empuja este frente de 6 pulgadas hacia adelante.
---
## Capacitancia distribuida de la línea de transmisión
Cuando hay varios conductores, existe capacitancia entre cada par. En las trazas de PCB, debido a la longitud de la estructura, cada parte de la traza tiene capacitancia con los conductores circundantes, por lo que la capacitancia de la línea de transmisión es distribuida. Mientras la señal avanza, experimenta la presencia de la capacitancia en cada paso.
En modelos de interconexión de alta velocidad, fenómenos como discontinuidades de impedancia, reflexiones y diafonía están relacionados con la capacitancia distribuida entre conductores.
## Capacitancia por unidad de longitud
En las líneas de transmisión de PCB, si el área transversal no cambia, puedes usar un modelo de capacitancia total, representando los parámetros de capacitancia por unidad de longitud. Esto hace que la capacitancia total sea proporcional a la longitud de la línea de transmisión, lo que facilita la modelización.
> Componentes totales: se refiere a componentes cuyo tamaño es mucho menor que la longitud de onda de las ondas electromagnéticas en relación con la frecuencia de funcionamiento de un circuito. Para las señales, las características del componente permanecen fijas en todo momento, independientemente de la frecuencia.
El uso de capacitancia por unidad de longitud para representar los efectos de capacitancia de la línea de transmisión se basa en la suposición de que no hay componentes del campo eléctrico a lo largo de la dirección de la línea de transmisión, es decir, la propagación de ondas electromagnéticas se aproxima a una onda plana uniforme. Las trazas de PCB cumplen con esta condición.
## Inductancia distribuida de la línea de transmisión
Las discontinuidades de impedancia, reflexiones, diafonía, ruido de tierra, y otros fenómenos están relacionados con la inductancia distribuida. Cada parte de las trazas de PCB tiene su propia inductancia y mutua inductancia con los conductores circundantes. La inductancia se distribuye en toda la longitud de la traza, y la señal la siente en cada paso.
## Inductancia de circuito
Espero que esta traducción sea de utilidad. Si tienes alguna pregunta adicional, no dudes en preguntar.
Dado que las líneas de transmisión pueden considerar las señales y las rutas de retorno como una entidad integral, donde la corriente de la señal y la corriente de retorno coexisten y forman un circuito completo de corriente, el análisis de la inductancia de bucle es más conveniente. La fórmula de cálculo de la inductancia de bucle es la siguiente:
Donde \(L_{\text{Ss}}\) representa la autoinductancia del camino de la señal, \(L_{\text{Fs}}\) representa la autoinductancia de la ruta de retorno y \(L_{\text{SFm}}\) es la mutua inductancia entre la señal y la ruta de retorno.
Cuando tratamos el circuito como una entidad integral, la inductancia de bucle describe las características de inductancia del circuito en sí, equivalente a su autoinductancia.
Inductancia por Unidad de Longitud
Para facilitar la modelización, la inductancia de la línea de transmisión se puede considerar equivalente a múltiples inductancias en serie. Dividimos la línea de transmisión en muchas secciones pequeñas de inductancia por unidad (cada sección incluye la señal y la ruta de retorno) con una longitud de \(\Delta Z\). A medida que \(\Delta Z\) aumenta, el área de la región formada por la señal y la ruta de retorno también aumenta, lo que resulta en un mayor flujo magnético. Dado que el flujo magnético está linealmente relacionado con el área de \(\Delta Z\), también está relacionado linealmente con \(\Delta Z\). Por lo tanto, si conocemos la inductancia por unidad de longitud, podemos obtener la inductancia de cualquier longitud.
Impedancia Transitoria e Impedancia Característica √
Según la definición anterior, sabemos que la impedancia se refiere a la relación entre el voltaje y la corriente en una ubicación específica de la línea de transmisión. Debido a que la línea de transmisión no es uniforme, la impedancia que la señal encuentra en cada paso puede ser diferente, lo que se conoce como impedancia transitoria.
Si la línea de transmisión es uniforme, entonces un solo valor de impedancia puede representar las características de impedancia de toda la línea de transmisión, y este valor se llama impedancia característica de la línea de transmisión. Puede expresarse en términos de inductancia por unidad de longitud y capacitancia por unidad de longitud de la siguiente manera:
El valor de 50Ω que a menudo se utiliza en el diseño de PCB se refiere a la impedancia característica. Para el material FR4, cuando el ancho de la línea es el doble del grosor del dieléctrico, la impedancia de una línea microstrip es de 50Ω. Cuando la distancia entre las líneas de transmisión es constante, un valor de impedancia característica más alto resulta en problemas de diafonía más graves, mientras que una impedancia característica más baja aumenta las pérdidas de potencia. Por lo tanto, 50Ω es un valor relativamente equilibrado y se ha convertido en un estándar general, pero no significa que todas las interconexiones deban ser de 50Ω; aún se pueden personalizar según sea necesario.
Factores que Afectan la Impedancia Característica √
Los principales factores que afectan la impedancia característica son 4: ancho de línea, grosor del dieléctrico, constante dieléctrica y grosor del cobre de las pistas.
El ancho de la línea afecta la inductancia y la capacitancia por unidad de longitud, lo que a su vez afecta la impedancia característica. Para la inductancia, un ancho de línea mayor resulta en una inductancia menor y una dispersión de corriente más amplia; mientras que un ancho de línea más estrecho concentra la corriente, lo que da como resultado una inductancia mayor. En cuanto a la capacitancia, un ancho de línea más grande significa que más líneas de flujo eléctrico entre la pista y el plano de tierra se concentran en la región del dieléctrico, lo que a su vez resulta en una capacitancia por unidad de longitud mayor (análogo a un condensador de placas paralelas: cuanto mayor es el área, mayor es la capacitancia); un ancho de línea más estrecho resulta en una capacitancia más baja. En resumen, un ancho de línea más ancho da como resultado una impedancia característica más baja.
El aumento del grosor del dieléctrico aumenta la separación entre los dos conductores, lo que reduce la mutua inductancia y aumenta la inductancia por unidad de longitud, lo que a su vez aumenta la impedancia característica de la línea de transmisión.
La constante dieléctrica afecta la capacitancia por unidad de longitud, ya que un aumento en la constante dieléctrica aumenta la capacitancia, lo que a su vez reduce la impedancia característica.
Un mayor grosor del cobre disminuye la inductancia y aumenta la capacitancia, lo que resulta en una impedancia característica más baja.
Impulsión y Resistencia Interna de la Línea de Transmisión
Un controlador se puede considerar como una fuente de voltaje de conmutación de alta velocidad con una resistencia interna:
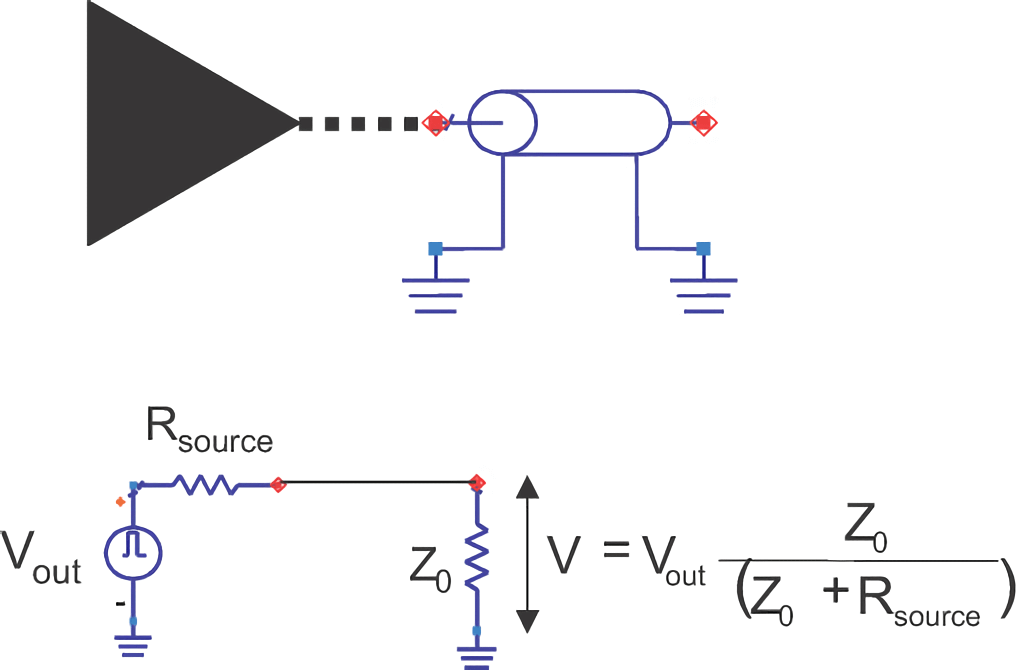
Cuando la línea de transmisión está en circuito abierto, el voltaje aplicado a la línea es muy cercano al voltaje fuente. La magnitud de la resistencia interna depende del proceso del dispositivo y generalmente se encuentra en el rango de 5-60Ω. Al agregar la resistencia interna en serie al circuito, se puede ver como un divisor de voltaje que genera una caída de voltaje.
Por lo tanto, para impulsar la línea de transmisión de manera efectiva, es importante que la resistencia interna del controlador sea lo más pequeña posible en comparación con la impedancia característica de la línea de transmisión. Por ejemplo, si la impedancia característica de la línea de transmisión es de 50Ω, la resistencia interna debe ser menor de 10Ω. Si la resistencia interna del controlador es muy baja, se le llama
Si el camino de retorno está en el mismo plano (diferente al de la vía de señal), se le llama plano de referencia. Para las líneas de señal de superficie, solo pueden formar líneas de transmisión con los planos internos adyacentes, por lo que se puede decir que las rutas de superficie tienen un solo plano de referencia. En cambio, para las rutas internas, hay dos planos adyacentes arriba y abajo, por lo que tienen dos planos de referencia. Los planos que se encuentran en diferentes capas y se superponen con las rutas de señal pueden utilizarse como planos de referencia, formando así líneas de transmisión.
La corriente de retorno en el plano de referencia no se distribuye uniformemente en todo el plano, sino que muestra un efecto de skin que se concentra cerca de la vía de señal. La magnitud de la corriente de retorno en el plano de referencia de las líneas de microstrip de superficie es igual a la corriente de señal. En el caso de las líneas stripline, dado que hay dos planos de referencia arriba y abajo, la corriente de retorno se concentra cerca de la parte superior e inferior de la vía de señal y se distribuye proporcionalmente según la distancia al plano. A medida que aumenta la frecuencia de la señal, la corriente se concentra aún más.
## Retraso en las líneas de transmisión 🚧
Las señales requieren un tiempo para viajar desde el punto de origen hasta el punto de destino, lo que introduce cierto retraso.
## Modelo de primer orden de una línea de transmisión ideal 🚧
Una línea de transmisión ideal tiene dos características clave: impedancia instantánea constante y retardo correspondiente. En el modelo de primer orden, basado en el modelo de cero orden, cada pequeño tramo de la señal y los conductores de retorno se abstraen como inductancia de bucle:
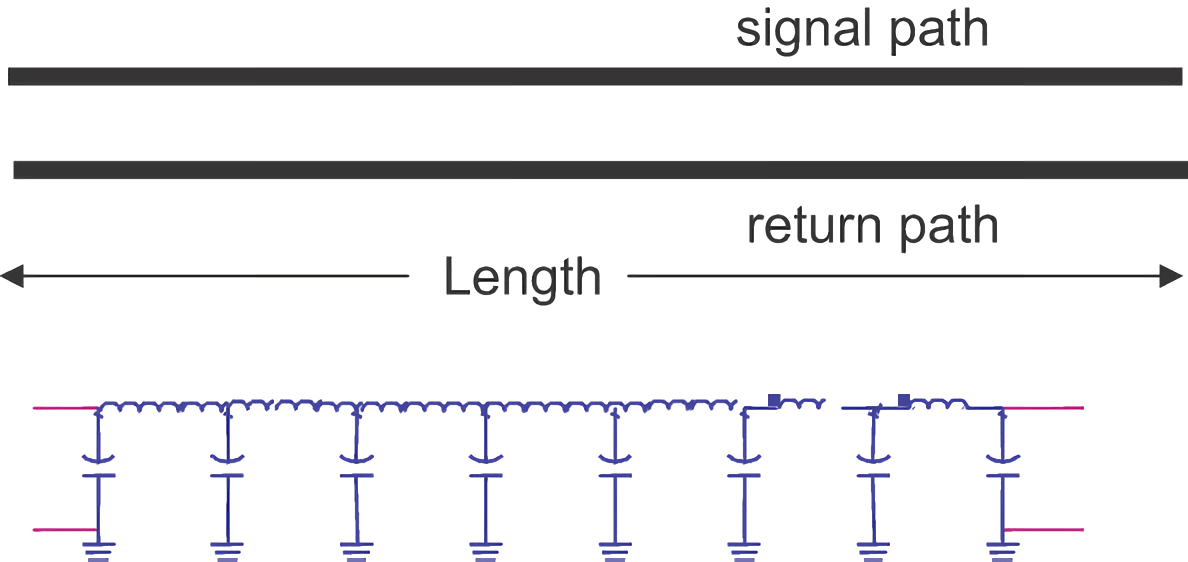
Cuando la capacitancia y la inductancia son infinitesimalmente pequeñas y el número de segmentos LC en el circuito tiende a infinito, la capacitancia por unidad de longitud $C_L$ y la inductancia por unidad de longitud $L_L$ tienden a constantes, que son los parámetros de línea de transmisión. Si la longitud total de la línea de transmisión es $Len$, la capacitancia total y la inductancia total son:
$$
C_{total}=C_L*Len
$$
$$
L_{total}=L_L*Len
$$
Por lo tanto, la impedancia característica $Z_0$ y el retardo $T_D$ de la línea de transmisión se calculan de la siguiente manera:
$$
Z_0=\sqrt{\frac{L_L}{C_L}}
$$
$$
T_D=\sqrt{C_{total}*L_{total}}=Len*\sqrt{C_L*L_L}
$$
$$
v=\frac{Len}{T_D}=\frac{1}{\sqrt{C_L*L_L}}
$$
Dado que la impedancia característica y el retardo de la línea de transmisión deben coincidir con los resultados del modelo de cero orden, se pueden obtener algunas ecuaciones relacionadas.
Dado que la velocidad de la señal depende de la constante dieléctrica $\varepsilon_r$ del material (epsilon), que a su vez depende de la capacitancia y la inductancia por unidad de longitud, se obtiene la siguiente ecuación:
$$
\because v=\frac{c}{\sqrt{\varepsilon_r}}=\frac{Len}{T_D}=\frac{1}{\sqrt{C_L*L_L}}
$$
## Referencias y Agradecimientos
- "Análisis de Integridad de Señal e Integridad de Alimentación"
- "Revelación de la Integridad de Señal - Notas de Diseño de SI del Dr. Yu"
> Dirección original del artículo: <https://wiki-power.com/>
> Este artículo está protegido por la licencia [CC BY-NC-SA 4.0](https://creativecommons.org/licenses/by/4.0/deed.zh). Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.