Radiofrecuencia - Componentes y Sistemas - Capacitores
Los capacitores también encuentran una amplia aplicación en el ámbito de la radiofrecuencia, como en desviaciones, acoplamientos inter-etapas, circuitos resonantes y filtros.
Capacitores de Placas Paralelas
Un capacitor es cualquier dispositivo compuesto por dos superficies conductoras separadas por un material aislante o dieléctrico. Los dieléctricos comúnmente utilizados son cerámica, aire, papel, mica, plástico, película delgada, vidrio o aceite. La capacidad de un capacitor es su capacidad para almacenar carga cuando hay una diferencia de potencial entre los conductores. La unidad de medida de la capacidad es el faradio (F).
Un capacitor consiste en dos superficies conductoras separadas por un dieléctrico. Los dieléctricos comunes incluyen cerámica, aire, papel, mica, plástico, película delgada, vidrio o aceite. La capacidad de un capacitor se refiere a su habilidad para almacenar carga cuando hay una diferencia de potencial entre los conductores. La capacidad se mide en faradios (F).
La capacidad se define mediante la siguiente fórmula:
Donde la capacidad \(C\) se mide en faradios (F) y la carga \(Q\) en culombios (C). Debido a que el faradio es una unidad grande, se utilizan subunidades como microfaradios (\(\mu\)F, \(10^{-6}\) F) y picofaradios (pF, \(10^{-12}\) F).
Si conocemos el área de las placas paralelas \(A\), la separación entre las placas \(d\) (en metros), y la constante dieléctrica del material \(\varepsilon\) (en faradios por metro), la fórmula para calcular la capacidad de un capacitor de placas paralelas se expresa como:
Donde \(\varepsilon_0\) es la constante dieléctrica del espacio libre (\(\varepsilon_0=8.854*10^{-12}\) F/m).
Circuitos Equivalentes de Capacitores
Los capacitores de placas paralelas son una idealización en la teoría, en el mundo real, los capacitores tienen un circuito equivalente como se muestra en la siguiente imagen:
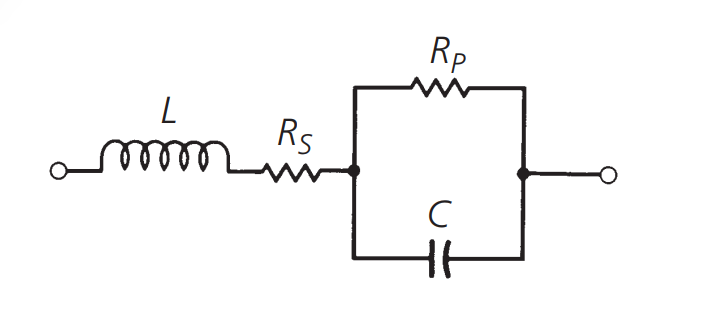
En esta representación, \(C\) es el capacitor propiamente dicho, \(L\) es la inductancia de los terminales, \(R_s\) es la pérdida de energía disipada, expresada en factor de potencia (FP) o factor de disipación (FD), y \(R_p\) representa la resistencia de aislamiento. Las definiciones más detalladas son las siguientes:
Factor de Potencia (Power Factor, PF):
En un capacitor ideal, la corriente alterna adelanta al voltaje aplicado en 90°. Sin embargo, debido a la resistencia total en el circuito equivalente (\(R_s + R_p\)), el ángulo de fase \(φ\) en un capacitor real será menor. El factor de potencia es una función de la temperatura, frecuencia y el material dieléctrico y se define mediante la siguiente fórmula:
Resistencia de Aislamiento (Insulation Resistance):
Representa la cantidad de corriente continua que fluye a través del dieléctrico del capacitor cuando se le aplica un voltaje. Ningún material es completamente aislante, por lo que hay una fuga de corriente. En el circuito equivalente, esta fuga se representa mediante \(R_p\), cuyo valor suele ser superior a 100,000 megohmios.
Resistencia en Serie Efectiva (Effective Series Resistance, ESR):
Este valor de resistencia es la combinación efectiva de \(R_s + R_p\) y representa la resistencia en corriente alterna del capacitor. Se define mediante la siguiente fórmula:
Donde \(\omega=2 \pi f\).
Factor de Disipación (Dissipation Factor, DF):
El factor de disipación es la relación entre la resistencia en corriente alterna y la reactancia del capacitor y se define mediante la siguiente fórmula:
El factor de calidad derivado de esto, Q, es el recíproco del factor de disipación. Cuanto mayor sea el valor de Q, mejor será el rendimiento del capacitor.
Los efectos de estas imperfecciones en un capacitor se pueden observar en la Figura 1-9. Aquí, se muestra cómo las características de impedancia de un capacitor ideal se comparan con las de un capacitor real. A medida que aumenta la frecuencia de operación, la inductancia del cableado se vuelve significativa. Finalmente, en la frecuencia resonante \(F_r\), la inductancia y el capacitor están en serie. Por encima de \(F_r\), el capacitor se comporta como un inductor. En general, los capacitores de mayor valor suelen tener más inductancia que los de menor valor.
En los capacitores reales, con estas influencias en cuenta, la curva de variación de frecuencia e impedancia se ve como se muestra en la siguiente imagen:
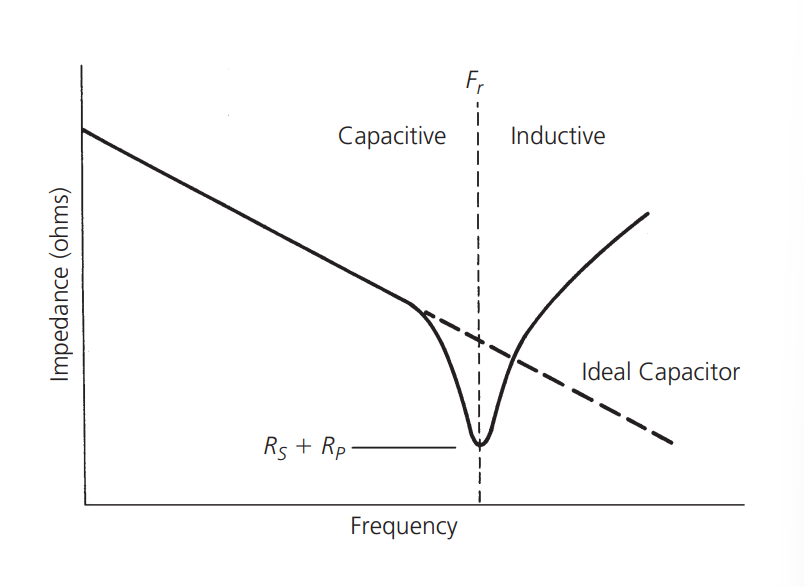
Puede verse que a medida que aumenta la frecuencia, la influencia de la inductancia de los terminales se hace más notable, y finalmente, en \(F_r\), la inductancia y el capacitor se vuelven resonantes en serie. A medida que la frecuencia aumenta aún más, el capacitor actúa como un inductor. En general, un capacitor de mayor valor suele tener más inductancia. Por lo tanto, en un ejemplo práctico, a una frecuencia de 250 MHz, un capacitor de 100 nF tendrá un efecto de desviación menos eficaz que uno de 300 pF, debido a la fórmula de reactancia \(X_c=\frac{1}{\omega C}\), que indica que, a una frecuencia dada, un capacitor de mayor valor tiene una menor reactancia.
Sin embargo, en cuanto a la frecuencia de radio, la situación podría ser justamente lo contrario. En ciertas frecuencias más altas, un condensador de 100nF podría presentar una mayor impedancia que uno de 330pF en relación a la señal. Esto es algo que debe considerarse al diseñar circuitos con frecuencias superiores a 100 MHz. Un analizador de redes puede revelar la impedancia del condensador a frecuencias específicas.
Tipos de Condensadores
Los condensadores pueden fabricarse con una variedad de materiales dieléctricos. Algunas de las categorías comunes incluyen:
(Por completar)
Referencias y Agradecimientos
- "RF-Circuit-Design (segunda edición) - Chris Bowick"
Dirección original del artículo: https://wiki-power.com/ Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.
Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.