Radiofrecuencia - Circuitos resonantes - Valor Q de carga 🚧
Definimos el valor Q de un circuito resonante como la relación entre la frecuencia central y el ancho de banda de atenuación de 3 dB, también conocido como valor Q de carga, ya que describe las características de paso del circuito resonante bajo condiciones de carga real o en el circuito. El valor Q de carga de un circuito resonante depende de tres factores principales:
- Impedancia de la fuente \(R_s\)
- Resistencia de carga \(R_L\)
- Valor Q de los componentes mencionados en el capítulo anterior
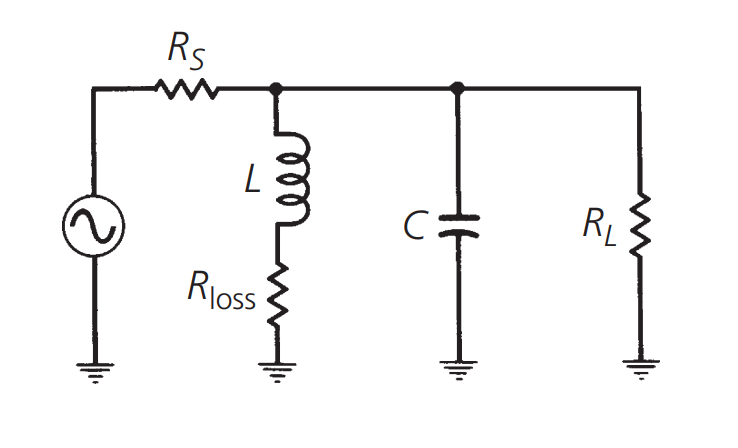
Influencia de \(R_s\) y \(R_L\) en el valor Q de carga
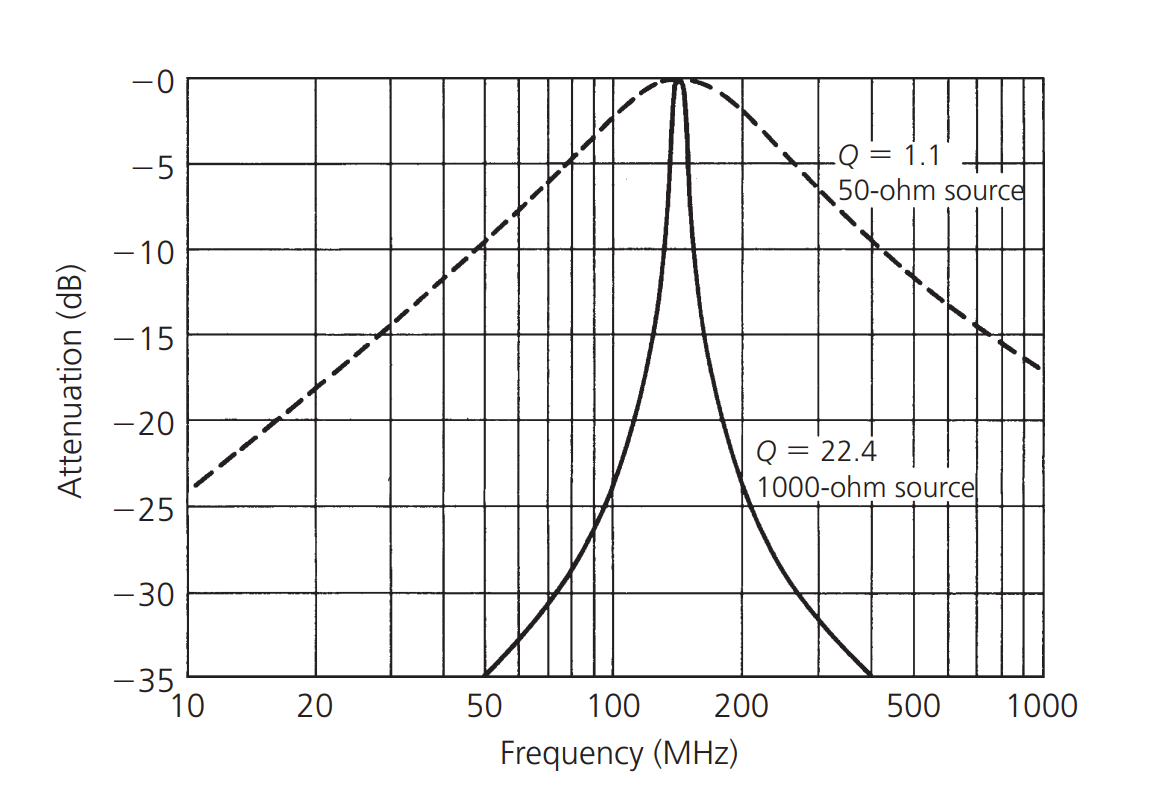
La influencia de la impedancia de la fuente y la impedancia de carga en el valor Q de carga del circuito resonante se muestra en el gráfico anterior. La curva original (línea punteada) es la curva de resonancia de un circuito compuesto por una impedancia de fuente de 50Ω, una inductancia sin pérdidas de 0.05uH y un capacitor sin pérdidas de 25pF. El valor Q calculado utilizando la fórmula mencionada anteriormente \(Q=\frac{f_e}{f_2-f_1}\) es aproximadamente 1.1, lo cual claramente no es un diseño de banda estrecha o alto valor Q.
Al cambiar la impedancia de la fuente a 1000Ω, se traza una nueva curva de resonancia (línea sólida) y el valor Q del circuito resonante aumenta significativamente a 22.4. Al aumentar la impedancia de la fuente, se incrementa el valor Q del circuito resonante.
El método anterior no muestra la influencia de la impedancia de carga en la curva de resonancia. Si se conecta una carga externa al circuito resonante de la siguiente manera:
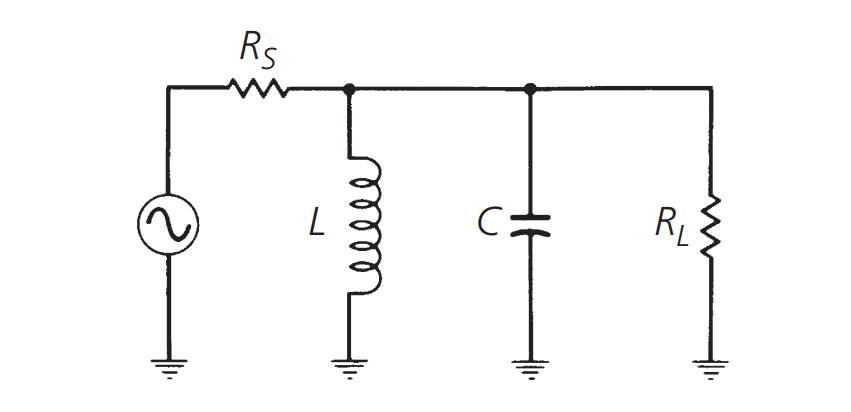
Puede ser equivalente a:
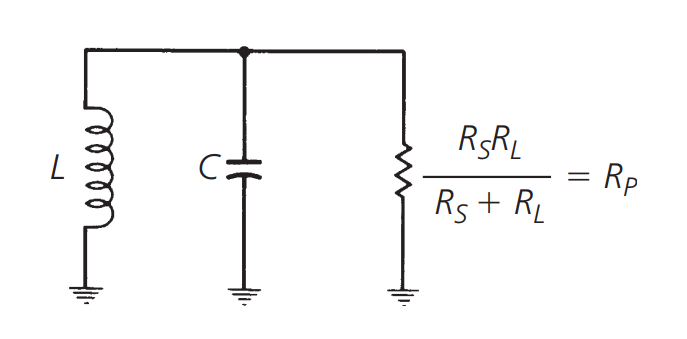
En este caso, el valor Q de carga se puede expresar como:
Donde \(R_p\) es la resistencia total equivalente en paralelo y \(X_p\) representa la reactancia / susceptancia (que son iguales en resonancia).
Por ejemplo, si queremos diseñar un circuito resonante que funcione bajo una impedancia de fuente de 150Ω y una impedancia de carga de 1000Ω. A una frecuencia de resonancia de 50 MHz, el valor Q de carga debe ser igual a 20. Supongamos que los componentes son sin pérdidas y no hay coincidencia de impedancia. Entonces podemos obtener \(R_p=130Ω\), según la fórmula mencionada anteriormente, \(X_p=\frac{R_p}{Q}=\frac{130}{20} =6.5Ω\), y como \(X_p=\omega L=\frac{1}{\omega C}\), podemos elegir una inductancia de 20.7nH y un capacitor de 489.7pF.
Se puede observar que la disminución de \(R_p\) reduce el valor Q del circuito resonante y, si \(R_p\) se mantiene constante y se cambia \(X_p\), se puede obtener el mismo efecto. Por lo tanto, para una impedancia de fuente y una impedancia de carga dadas, se puede obtener el mejor valor Q del circuito resonante cuando la inductancia es pequeña y el capacitor es grande. En ambos casos, \(X_p\) disminuirá. Por ejemplo:
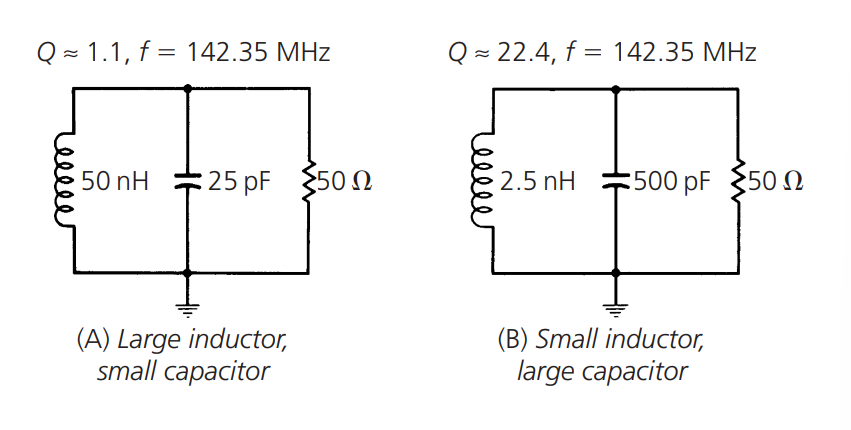
Por lo tanto, se pueden utilizar ambos métodos para ajustar el valor Q:
- Seleccionar los mejores valores para la impedancia de la fuente y la impedancia de carga.
- Seleccionar los valores óptimos de los componentes L y C para optimizar el valor Q.
Sin embargo, generalmente solo podemos utilizar el segundo método, ya que en muchos casos, la fuente y la carga están fijas y no se pueden cambiar. En esta situación, \(X_p\) se define por un valor Q dado, pero generalmente el valor calculado no tiene un valor físico adecuado para que coincida. Se proporcionará una solución a este problema en el siguiente texto.
Influencia del valor Q de los componentes en el valor Q de carga
En los párrafos anteriores, hemos asumido que los componentes utilizados en el circuito resonante son componentes sin pérdidas y que el valor Q de los componentes no afecta el valor Q de carga. Sin embargo, en situaciones no ideales, debemos considerar el valor Q de cada componente individual.
En un circuito resonante sin pérdidas, la impedancia en los terminales del circuito en resonancia es infinita. Pero en un circuito real, debido a las pérdidas en los componentes, habrá alguna resistencia en paralelo equivalente:
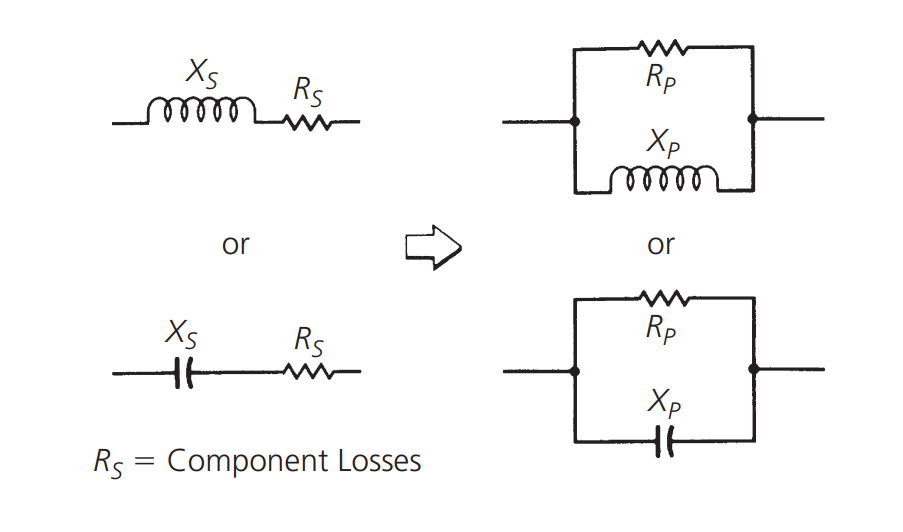
La resistencia (Rp) y su reactancia en paralelo relacionada (Xp) se pueden obtener a partir de
Referencias y agradecimientos
- 《RF-Circuit-Design(second-edition)_Chris-Bowick》
Dirección original del artículo: https://wiki-power.com/
Este artículo está protegido por la licencia CC BY-NC-SA 4.0. Si desea reproducirlo, por favor indique la fuente.Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.