ADC - Parámetros Estáticos
El Convertidor Analógico a Digital (ADC, por sus siglas en inglés) es un dispositivo que convierte señales analógicas en una secuencia de datos digitales.
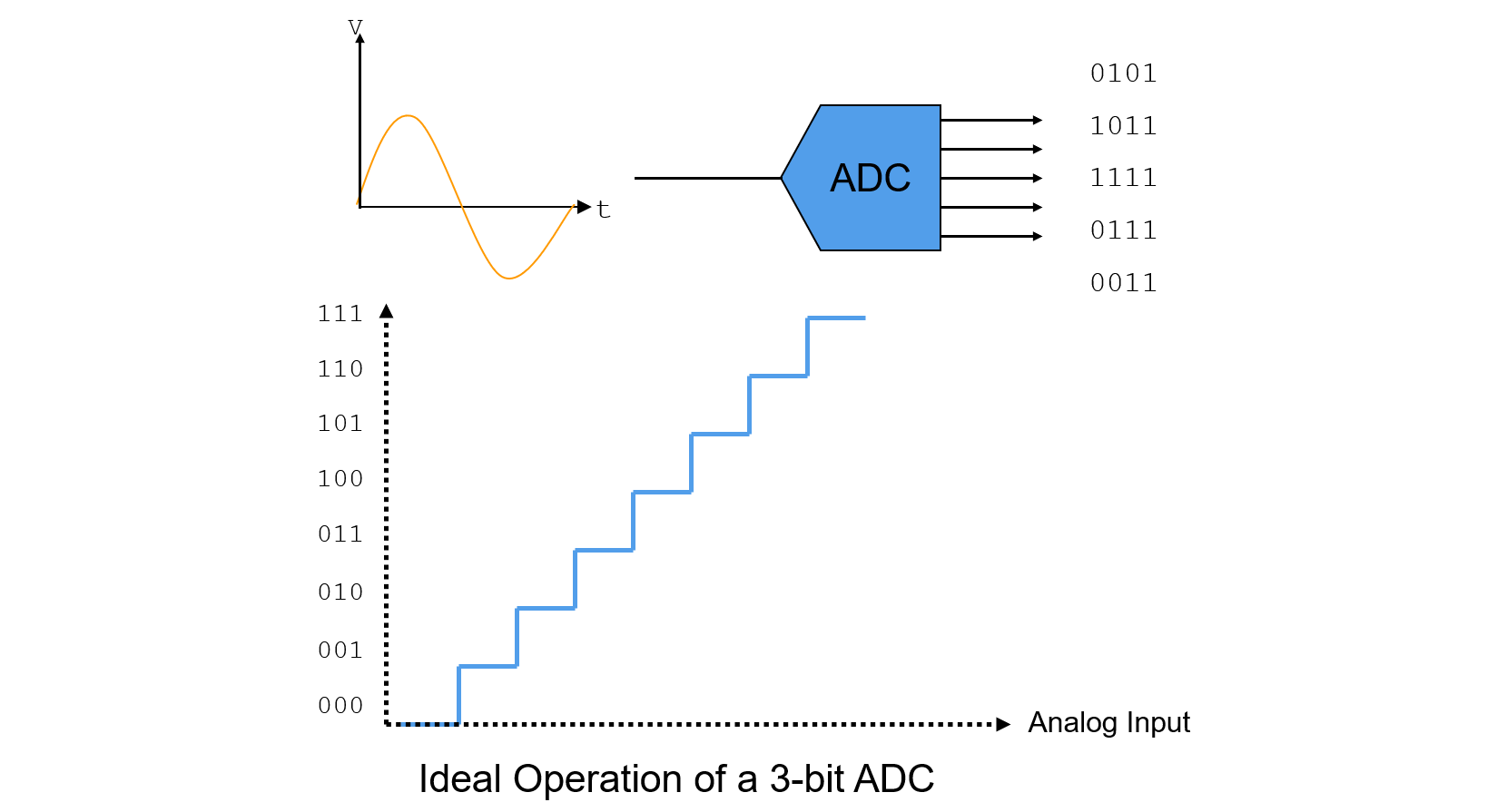
Aunque la función de transferencia ideal de un ADC debería ser una línea recta, en realidad es una escalera uniforme, donde el número de escalones corresponde al número de códigos de salida digitales. Dado que lo analógico es continuo y lo digital es discreto, se introduce un error de cuantización en el procedimiento.
Parámetros Estáticos
Los parámetros estáticos de un ADC principalmente incluyen:
- Tamaño del LSB
- Rango de Escala Completa (FSR, por sus siglas en inglés)
- Error de Desplazamiento
- Error de Ganancia
- Error de No Linealidad Diferencial (DNE o DNL, por sus siglas en inglés)
- Error de No Linealidad Integral (INE o INL, por sus siglas en inglés)
Tamaño del LSB
El ancho de un escalón se define como 1 Bit Menos Significativo (LSB, por sus siglas en inglés). La resolución de un ADC se expresa normalmente en número de bits (código de salida digital). Un ADC con una resolución de n bits tiene \(2^n\) posibles códigos digitales (\(2^n\) niveles de escalón).
Para un ADC ideal, el LSB representa todo el ancho de cada código.
Rango de Escala Completa (FSR)
Por ejemplo, para un convertidor de 3 bits, hay:
- 8 escalones horizontales
- 7 transiciones
- 6 escalones entre 7 transiciones
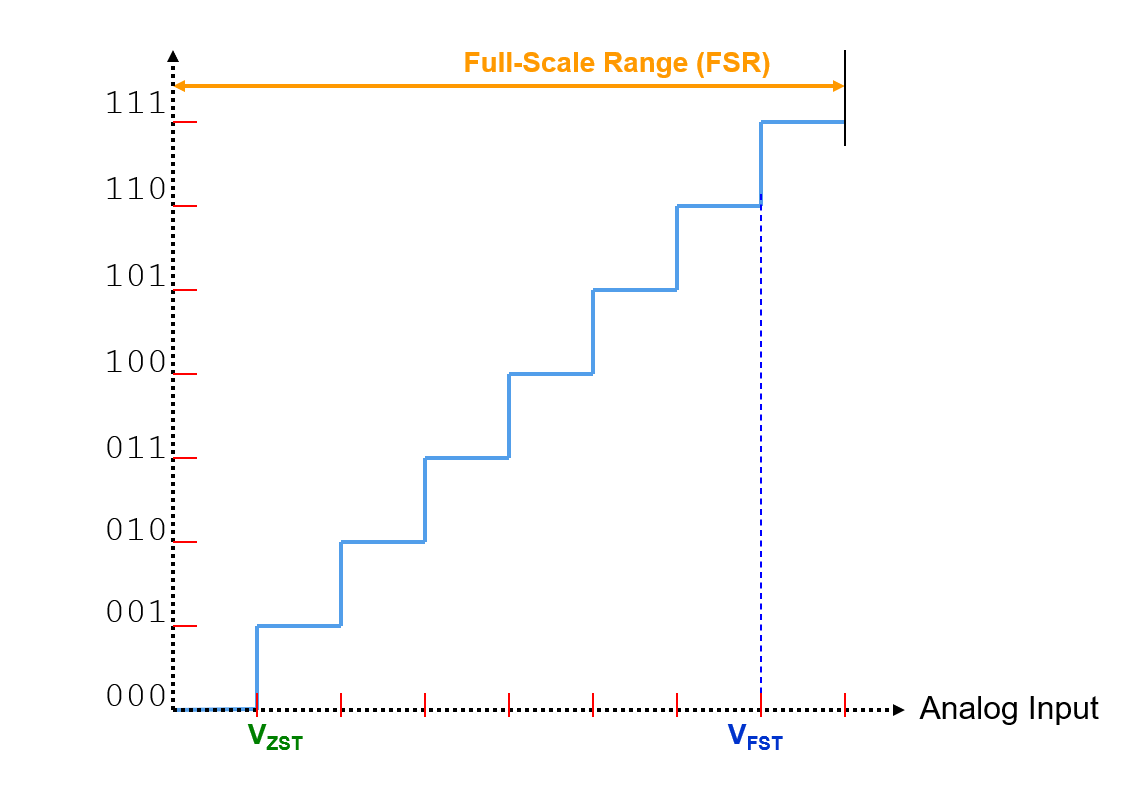
- Voltaje de Transición de Rango Cero (\(V_{ZST}\)): Voltaje de la señal de entrada analógica cuando se registra la primera transición.
- Voltaje de Transición de Rango Completo (\(V_{FST}\)): Voltaje de la señal de entrada analógica cuando se registra la última transición.
- Rango de Escala Completa (FSR): Extremo máximo de la señal de entrada analógica suministrada al ADC. \(FSR = (V_{FST}-V_{ZST}) + 2 LSB\), \(V_{FSR(refer to VZS)} = (V_{FST}-0.5LSB)-(V_{ZST}-0.5LSB) + 2 LSB\)
Error de Desplazamiento
Error de Desplazamiento (Error de Cero) es la diferencia entre los puntos de desplazamiento (inicial) ideal y real. Se mide desde el punto medio del paso cero (ideal a real) para el ADC.
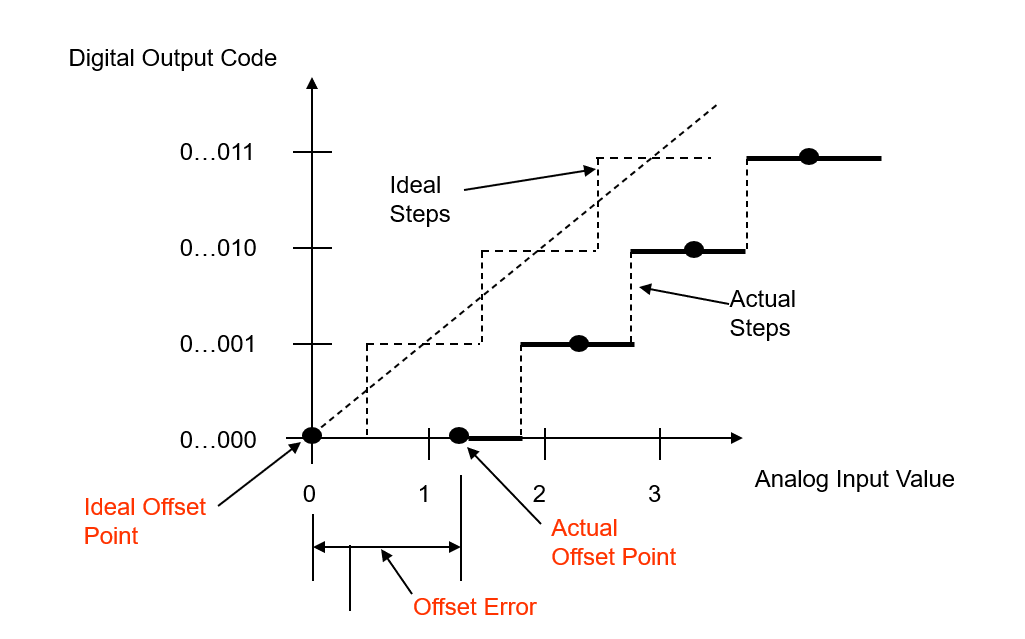
Donde
Error de Ganancia
Error de Ganancia es la diferencia entre los puntos de ganancia ideal y real en la función de transferencia (después de corregir el error de desplazamiento a cero). Se mide desde el punto medio del paso completo para el ADC.
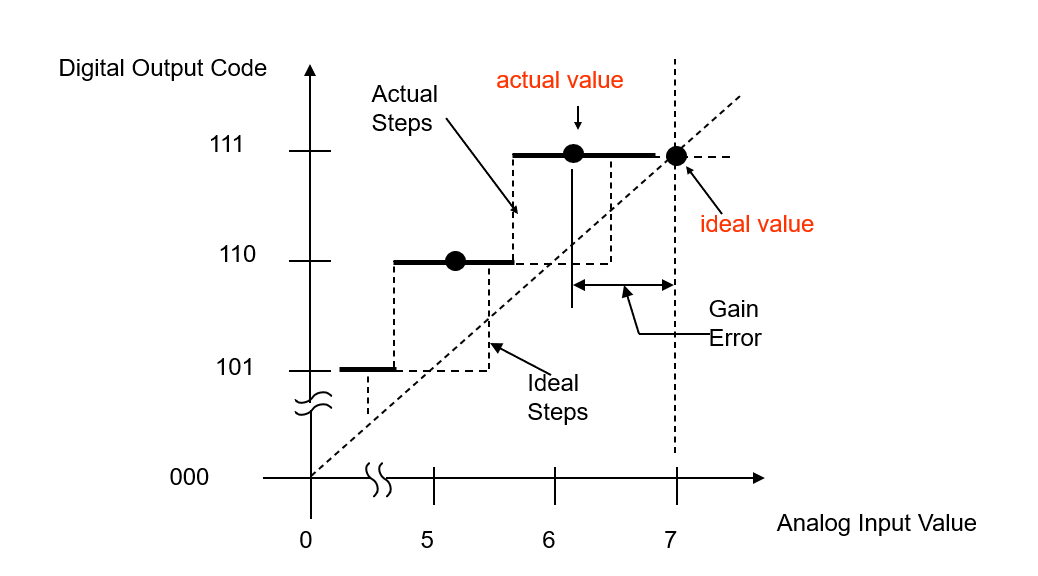
Donde
Error de No Linealidad Diferencial (DNL)
Error de No Linealidad Diferencial (DNL) es la diferencia entre el ancho de paso real y el ancho de paso ideal (1 LSB). Es una medida del error de linealidad "de pequeña señal" y se mide a partir de la diferencia en el voltaje de entrada analógico entre dos transiciones adyacentes y el LSB promedio del dispositivo.
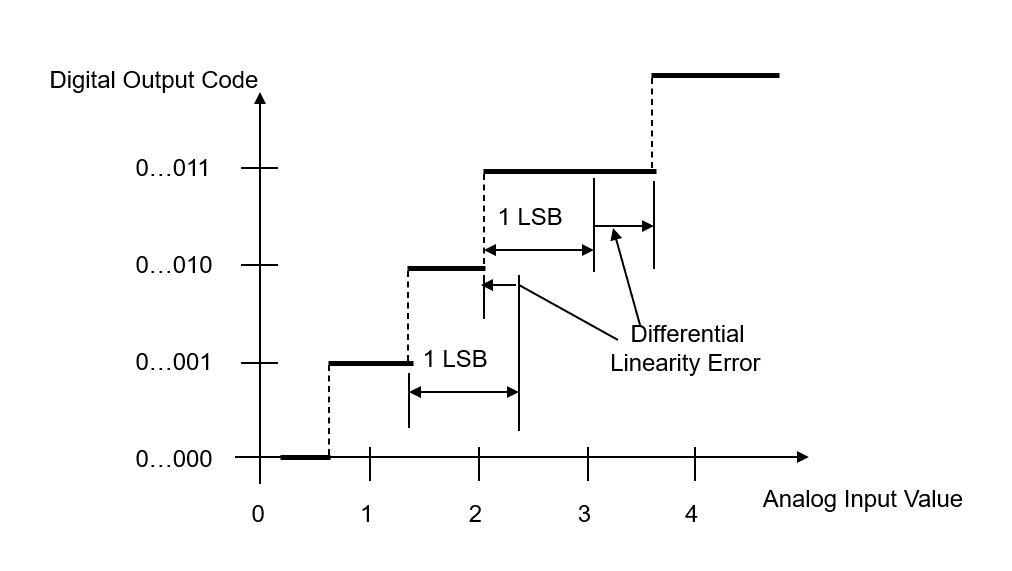
Ecuaciones para describir DNL:
otra imagen para describir DNL:
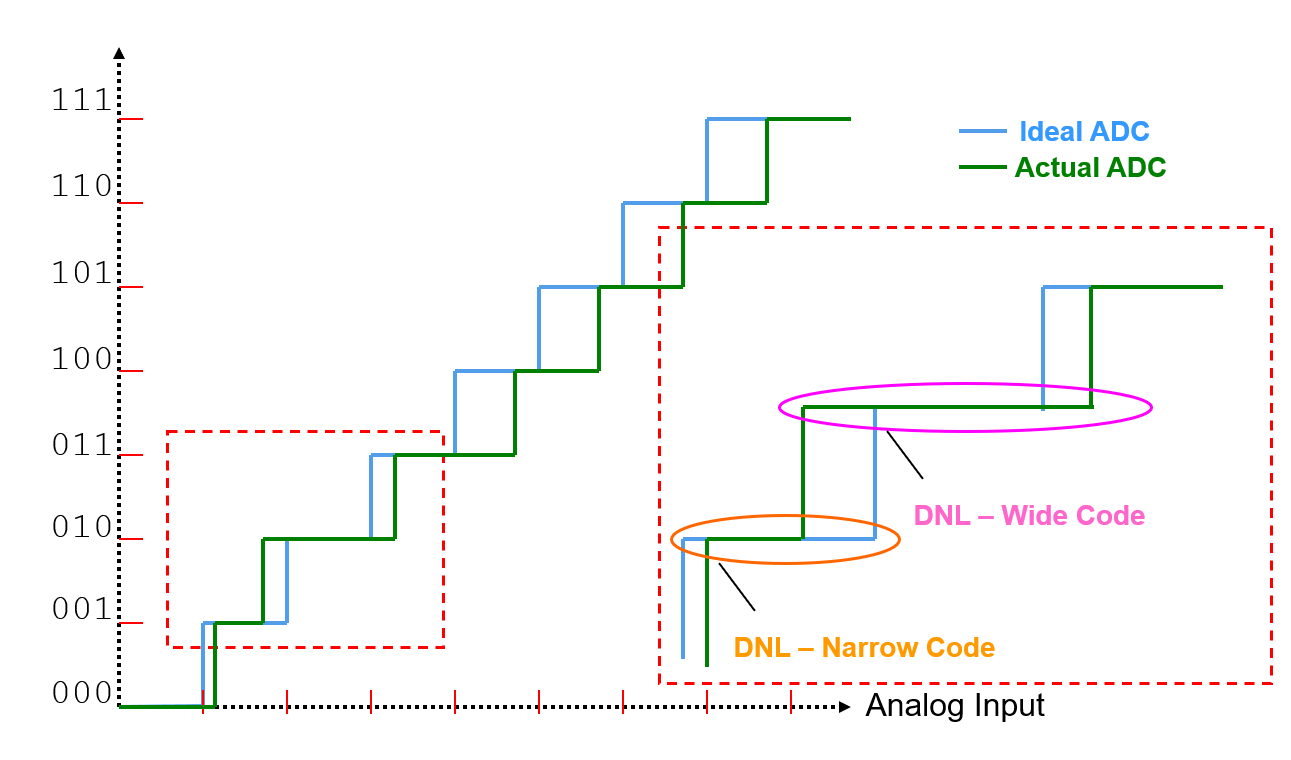
Si el DNL es demasiado grande, faltará uno o más códigos y nunca se recibirá una salida.
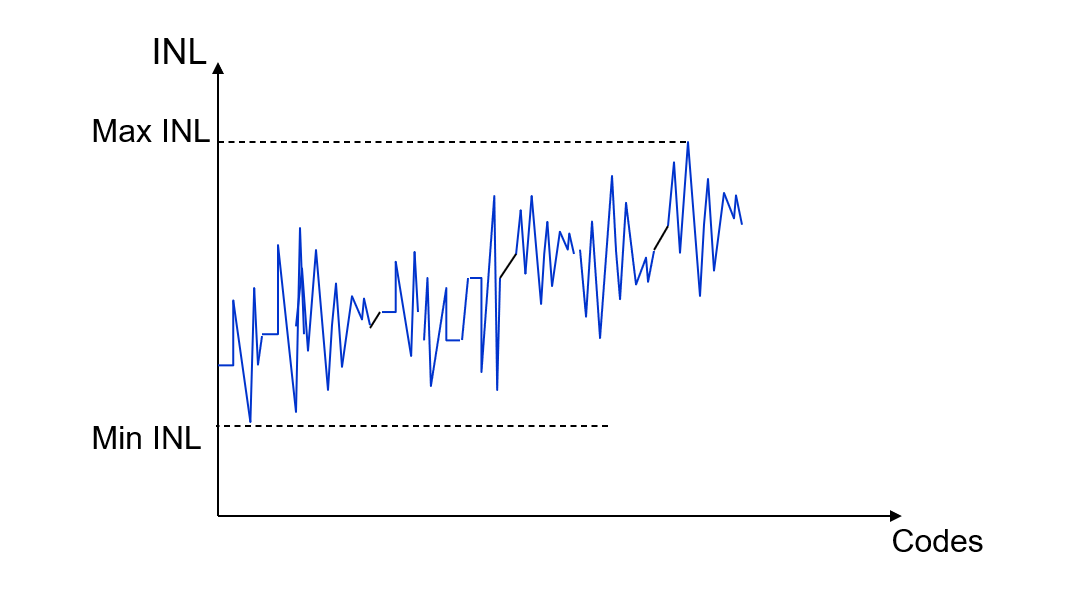
Error de No Linealidad Integral (INL)
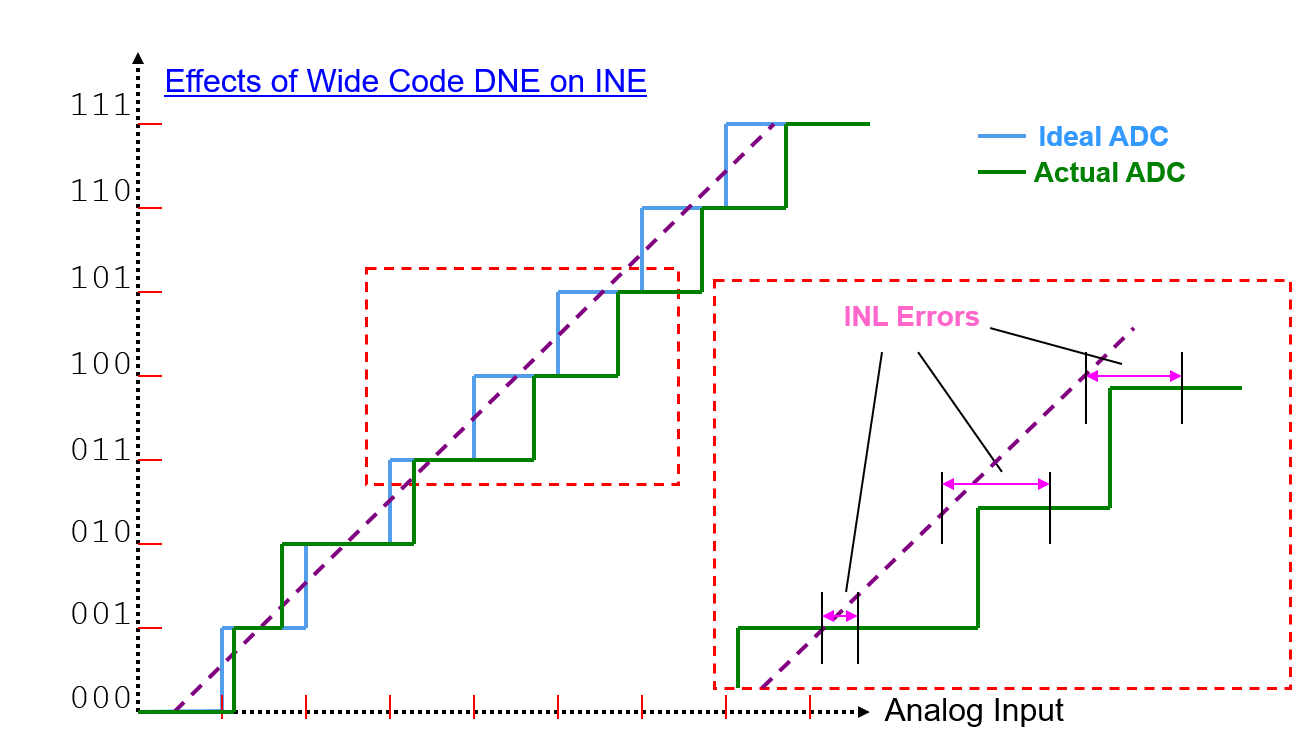
Error de No Linealidad Integral (INL) es el efecto acumulativo en cualquier entrada dada de todos los valores de no linealidad diferencial. Es una medida del error de linealidad "de gran señal". El INL en cualquier punto a lo largo de la curva es la desviación de la línea de linealidad ideal.
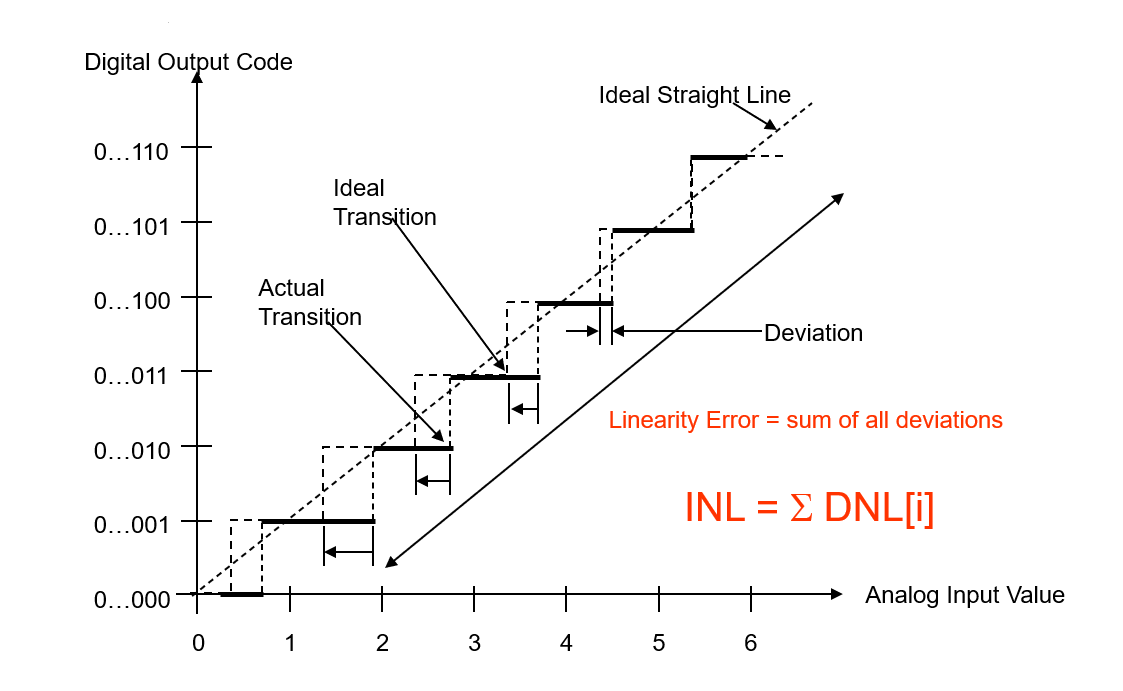
Las desviaciones se miden en los puntos de transición de un paso al siguiente para el ADC. INL es la desviación de los valores de la función de paso real con respecto a la función de línea recta ideal.
Ecuaciones para describir INL:
Cómo probar los parámetros estáticos
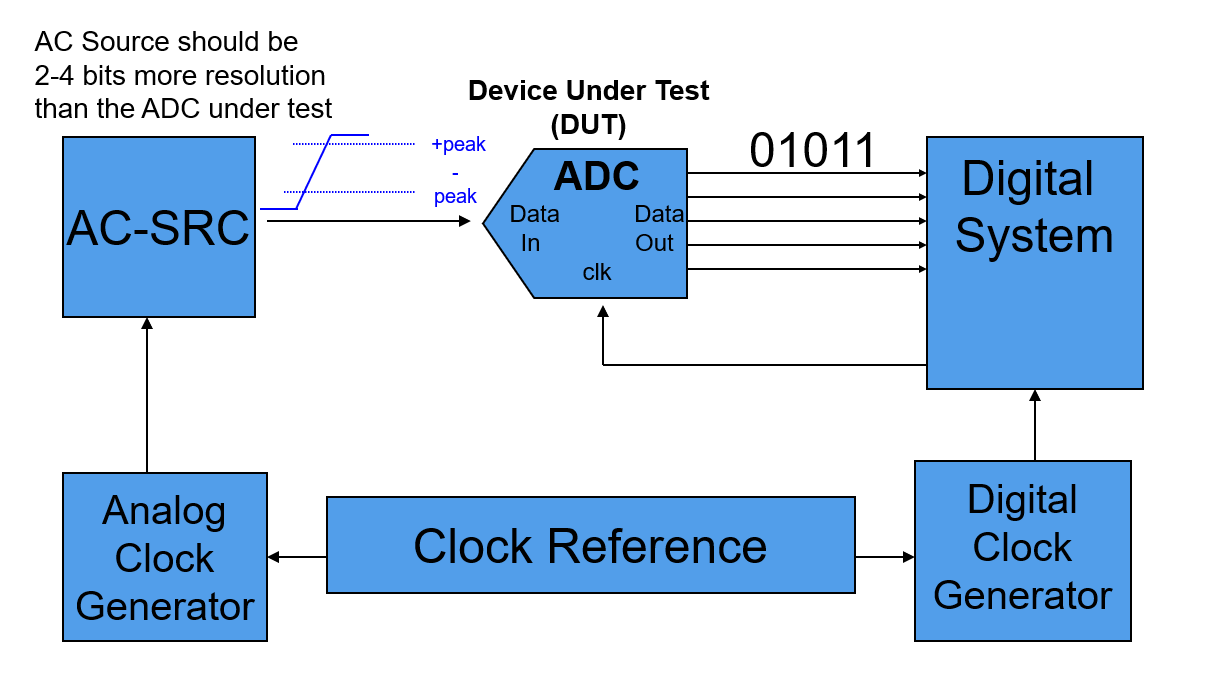
Configuración del sistema de prueba
Configuración del sistema de prueba para las pruebas de parámetros estáticos del ADC:
Dado que la curva de transferencia de voltaje a código del ADC es una función de mapeo de muchos a uno:
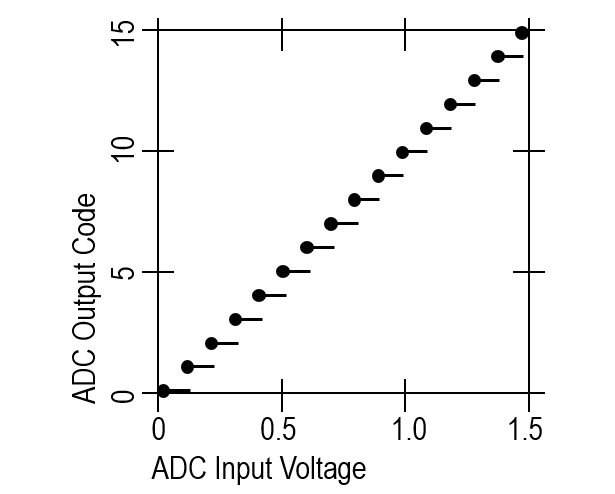
Prácticamente, utilizamos el método del histograma de rampa lineal (medición del ancho del código). La rampa de entrada es lo suficientemente lenta como para proporcionar un "número estadísticamente relevante de aciertos por código".
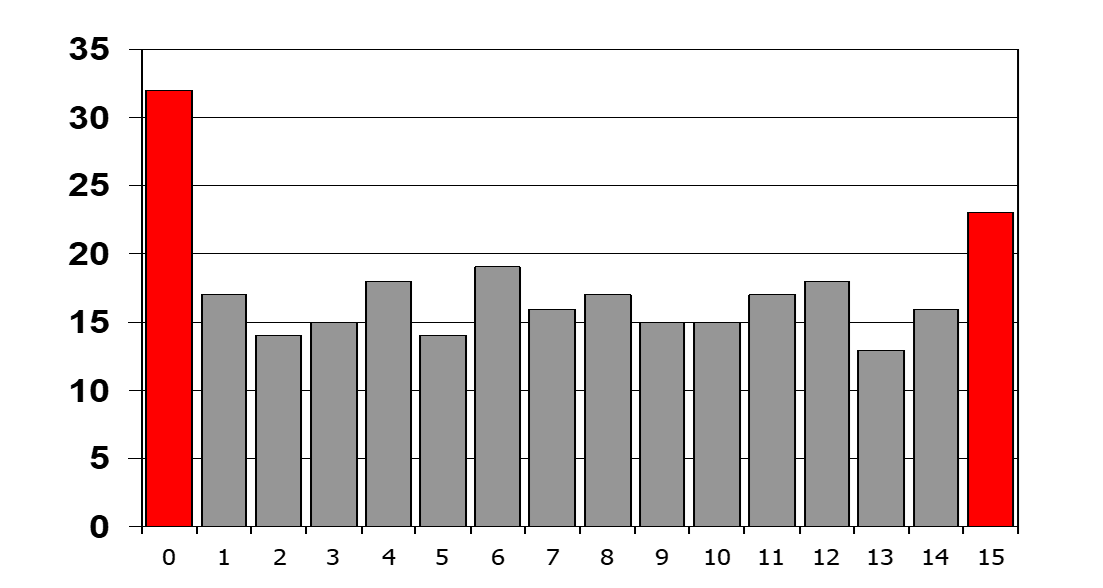
Diagrama de bloques de la configuración de la señal:
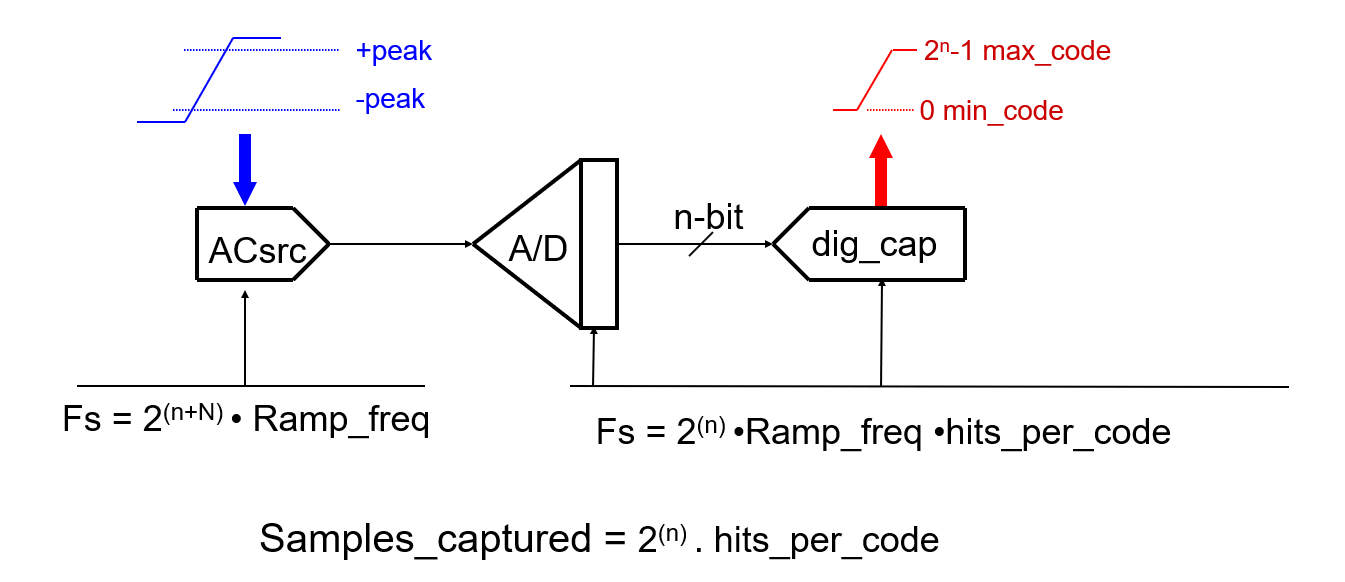
Concepto de las pruebas
El procedimiento para probar los parámetros estáticos de un ADC DUT se enumera a continuación.
1. Crear un segmento de onda de rampa para AC SRC
La rampa de entrada va por encima y por debajo de ±Fs para asegurar que se cubran todos los códigos:
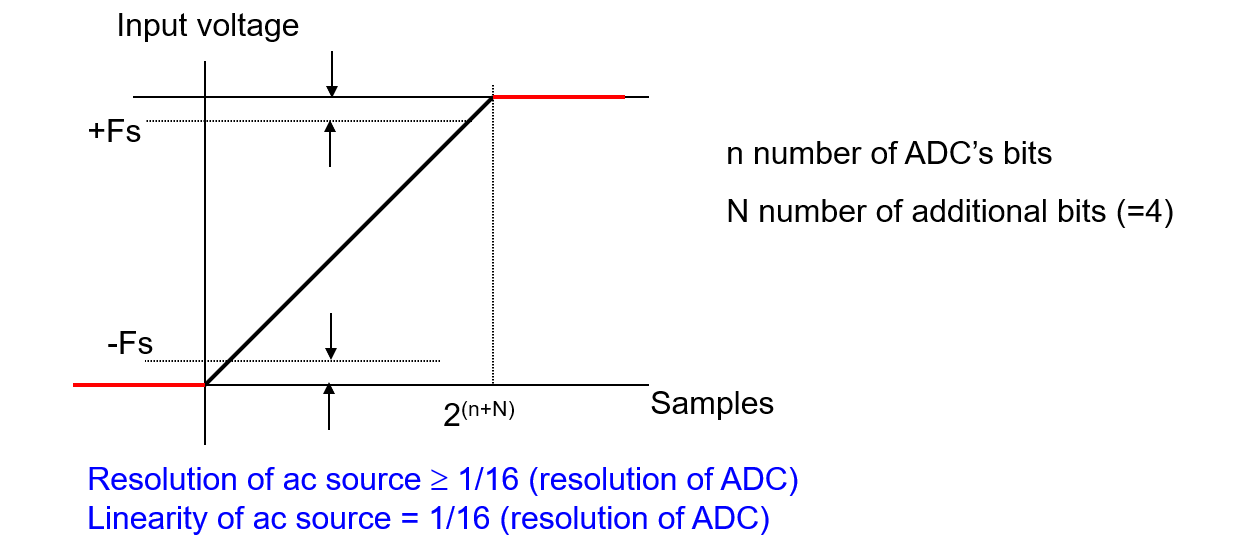
2. Tomar datos entre el inicio (min+1, por ejemplo, 0...01) y el final (max-1, por ejemplo, 1...10) de la rampa. Esto proporciona datos equivalentes a \(2^n – 2\) códigos
El voltaje aplicado debe ser más amplio que el rango de escala completa para cubrir todas las transiciones. A continuación se muestra un ejemplo con 16 pasos entre cada transición de código:
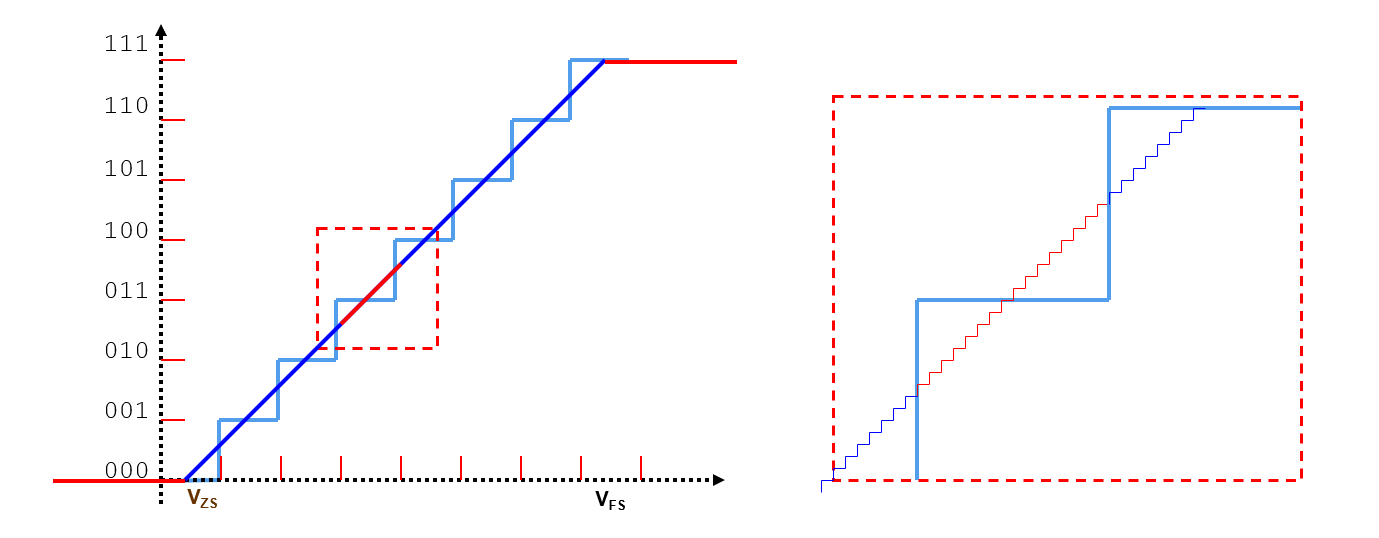
para el ADC DUT ideal, 16 códigos de salida aparecen al mismo tiempo:
Sin embargo, un dispositivo real tendrá un recuento más de 16 veces para códigos más anchos y menos de 16 veces para los más estrechos (pero la suma del total de ocurrencias debería seguir siendo \(2^{bits}\) veces 16):
3. Calcular el DNL para cada paso
Donde \(Hits[i]\) representa el recuento real del código de salida y \(\frac{\sum Hits[i]}{2^n-2}\) representa el recuento ideal del código de salida.
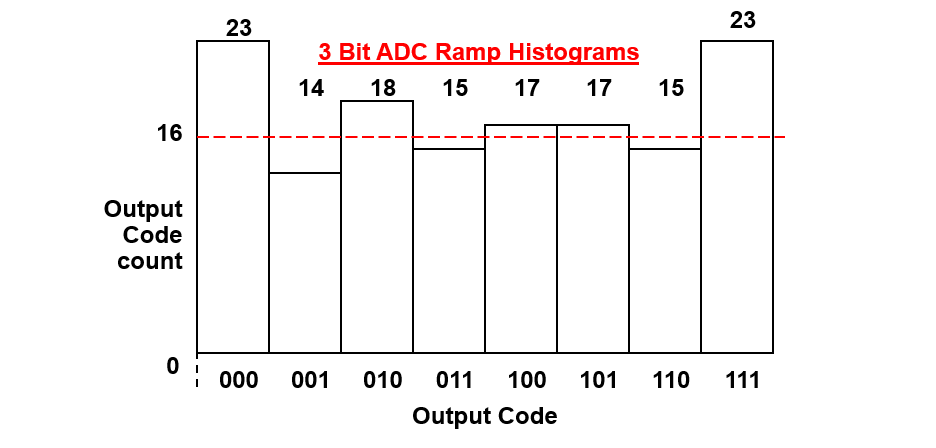
Para un ejemplo de gráfico de histograma como se muestra a continuación:
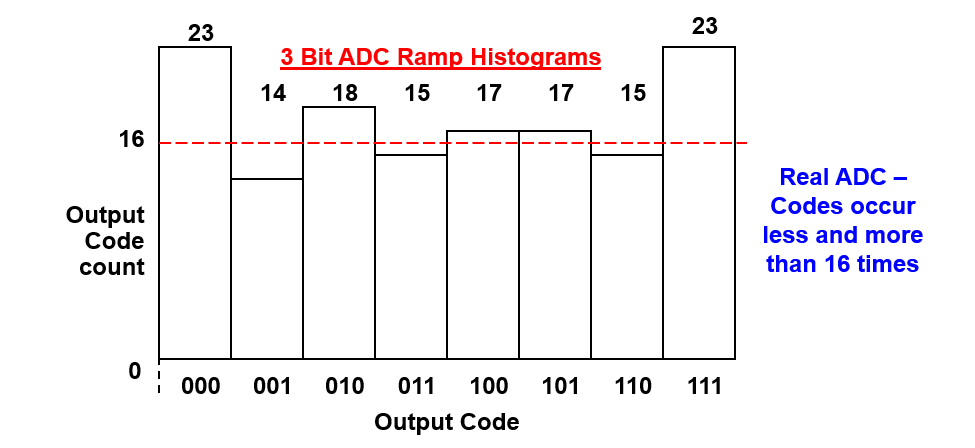
para \(DNL[1](Código 001)\),
- Recuento real del código de salida = 14
- Recuento ideal del código de salida = (14 +18 +15 + 17+ 17 + 15) / (8 -2 ) = 16.
Por lo tanto, \(DNL[1] (Código 001) = (14-16)/16 \ LSB => -0.125 \ LSB\).
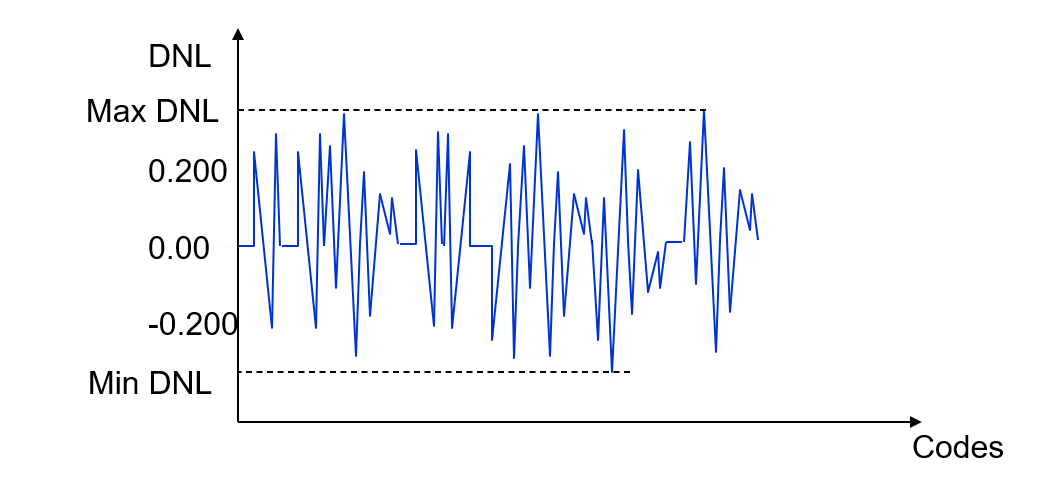
4. Obtener el DNL máximo y mínimo
5. Calcular el INL para cada paso
INL es el valor acumulativo del primer DNL hasta el DNL[i] (excepto el DNL de cero y de escala completa):
Tenga en cuenta que \(DNL[0]\) no se utiliza,
Para un ejemplo de gráfico a continuación,
6. Obtener el INL máximo y mínimo
Referencias y Agradecimientos
- Fundamentals of Testing Using ATE
- The-Fundamentals-of-Mixed-Signal-Testing_Brian-Lowe
Original: https://wiki-power.com/
Este artículo está protegido por el acuerdo CC BY-NC-SA 4.0, y debe ser reproducido con atribución.Este post está traducido usando ChatGPT, por favor feedback si hay alguna omisión.